Một phép chiếu song song biến tam giác ABC thành tam giác A'B'C'. Chứng minh rằng phép chiếu đó biến đường trung bình của tam giác ABC

Luyện tập 3 trang 98 Toán 11 Tập 1: Một phép chiếu song song biến tam giác ABC thành tam giác A'B'C'. Chứng minh rằng phép chiếu đó biến đường trung bình của tam giác ABC thành đường trung bình của tam giác A'B'C'.

Trả lời

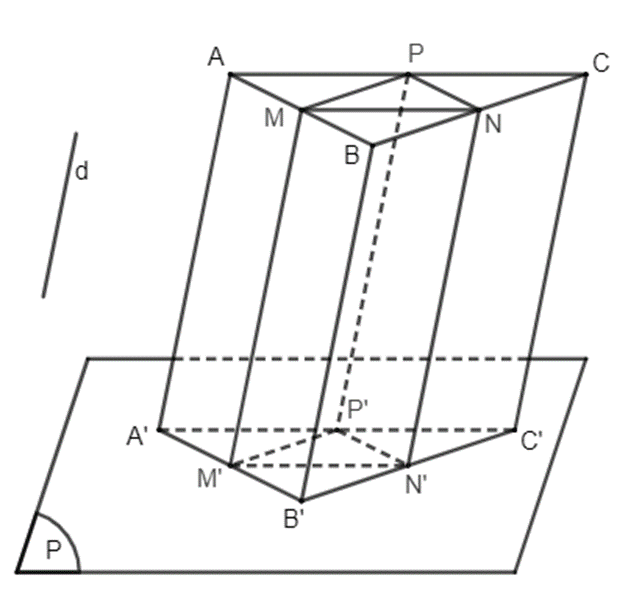
Tam giác A'B'C' là hình chiếu của tam giác ABC trên mặt phẳng (P) theo phương d.

Gọi M, N, P lần lượt là trung điểm của AB, BC, AC. Khi đó MN, NP, MP là các đường trung bình của tam giác ABC.

Gọi M', N', P' lần lượt là hình chiếu của M, N, P trên mặt phẳng (P) theo phương d.

Vì M là trung điểm của AB nên A, M, B thẳng hàng theo thứ tự đó và $\frac{AM}{MB}=1$ . Do vậy A', M', B' thẳng hàng theo thứ tự đó và $\frac{A^{\text{'}}{M}^{\text{'}}}{M^{\text{'}}{B}^{\text{'}}}=1$ , tức là M' là trung điểm của A'B'. Chứng minh tương tự ta có N' là trung điểm của B'C' và P' là trung điểm của A'C'. Vậy M'N', N'P', M'P' là các đường trung bình của tam giác A'B'C'.

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số