Câu hỏi:
29/12/2023 194
Một nhóm học sinh gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập đội cờ đỏ?
Một nhóm học sinh gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một đội cờ đỏ sao cho phải có 1 đội trưởng nam, 1 đội phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập đội cờ đỏ?
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:
• Trường hợp 1: chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữ: 5 cách
+) Số cách chọn 2 nam làm đội trưởng và đội phó: \(A_{15}^2\)
+) Số cách chọn 2 nam còn lại: \(C_{13}^2\)
Suy ra có \(5A_{15}^2.C_{13}^2\) cách chọn cho trường hợp này.
• Trường hợp 2: chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: \(C_5^2\) cách.
+) Số cách chọn 2 nam làm đội trưởng và đội phó: \(A_{15}^2\)cách.
+) Số cách chọn 1 còn lại: 13 cách.
Suy ra có \[13A_{15}^2.C_5^2\] cách chọn cho trường hợp này.
• Trường hợp 3: Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ : \(C_5^3\) cách.
+) Số cách chọn 2 làm đội trưởng và đội phó: \(A_{15}^2\) cách.
Suy ra có \(A_{15}^2.C_5^3\) cách chọn cho trường hợp 3.
Vì các trường hợp là rời nhau. Vậy nên ta có \(5A_{15}^2.C_{13}^2 + 13A_{15}^2.C_5^2 + A_{15}^2.C_5^3 = 111\,300\) cách.
Vì trong 5 người được chọn phải có ít nhất 1 nữ và ít nhất phải có 2 nam nên số học sinh nữ gồm 1 hoặc 2 hoặc 3 nên ta có các trường hợp sau:
• Trường hợp 1: chọn 1 nữ và 4 nam.
+) Số cách chọn 1 nữ: 5 cách
+) Số cách chọn 2 nam làm đội trưởng và đội phó: \(A_{15}^2\)
+) Số cách chọn 2 nam còn lại: \(C_{13}^2\)
Suy ra có \(5A_{15}^2.C_{13}^2\) cách chọn cho trường hợp này.
• Trường hợp 2: chọn 2 nữ và 3 nam.
+) Số cách chọn 2 nữ: \(C_5^2\) cách.
+) Số cách chọn 2 nam làm đội trưởng và đội phó: \(A_{15}^2\)cách.
+) Số cách chọn 1 còn lại: 13 cách.
Suy ra có \[13A_{15}^2.C_5^2\] cách chọn cho trường hợp này.
• Trường hợp 3: Chọn 3 nữ và 2 nam.
+) Số cách chọn 3 nữ : \(C_5^3\) cách.
+) Số cách chọn 2 làm đội trưởng và đội phó: \(A_{15}^2\) cách.
Suy ra có \(A_{15}^2.C_5^3\) cách chọn cho trường hợp 3.
Vì các trường hợp là rời nhau. Vậy nên ta có \(5A_{15}^2.C_{13}^2 + 13A_{15}^2.C_5^2 + A_{15}^2.C_5^3 = 111\,300\) cách.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1) và C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3; – 1) và B(– 6; 2). Phương trình nào sau đây không phải là phương trình tham số của đường thẳng AB?
Câu 3:
Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
Tọa độ giao điểm của hai đường thẳng x – 3y – 6 = 0 và 3x + 4y – 1 = 0 là
Câu 4:
Có bao nhiêu cách xếp 5 người ngồi vào một dãy ghế gồm có 6 chiếc ghế, biết mỗi người ngồi vào một ghế.
Có bao nhiêu cách xếp 5 người ngồi vào một dãy ghế gồm có 6 chiếc ghế, biết mỗi người ngồi vào một ghế.
Câu 5:
Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\) và d2: mx + 2y – 14 = 0. Giá trị của m để hai đường thẳng trên song song với nhau là
Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 8 - \left( {m + 1} \right)t\\y = 10 + t\end{array} \right.\) và d2: mx + 2y – 14 = 0. Giá trị của m để hai đường thẳng trên song song với nhau là
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng d là
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: – x + 2y + 7 = 0. Vectơ pháp tuyến của đường thẳng d là
Câu 7:
Cho đường thẳng d1: 2x – y – 2 = 0; d2: x + y + 3 = 0 và điểm M(3; 0). Viết phương trình đường thẳng ∆ đi qua điểm M, cắt d1 và d2 lần lượt tại A và B sao cho M là trung điểm của đoạn AB.
Cho đường thẳng d1: 2x – y – 2 = 0; d2: x + y + 3 = 0 và điểm M(3; 0). Viết phương trình đường thẳng ∆ đi qua điểm M, cắt d1 và d2 lần lượt tại A và B sao cho M là trung điểm của đoạn AB.
Câu 8:
Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
Khoảng cách từ điểm M(5; – 1) đến đường thẳng d: 3x + 2y + 13 = 0 là
Câu 9:
Một lớp có 40 học sinh gồm 25 nam và 15 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học sinh trong đó có ít nhất một học sinh nữ?
Một lớp có 40 học sinh gồm 25 nam và 15 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học sinh trong đó có ít nhất một học sinh nữ?
Câu 10:
Cho tập hợp H = {1; 3; 5; 7; 9; 11}. Một tổ hợp chập 3 của 6 phần tử của H là
Cho tập hợp H = {1; 3; 5; 7; 9; 11}. Một tổ hợp chập 3 của 6 phần tử của H là
Câu 11:
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
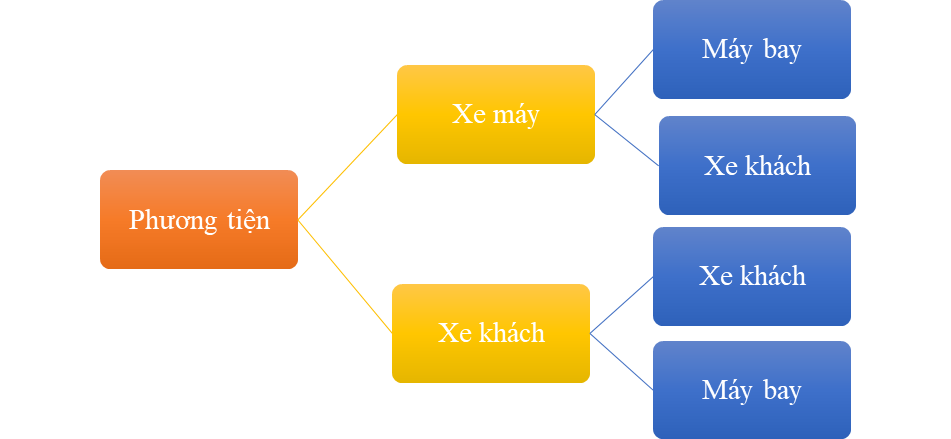
Hỏi bạn Khoa có mấy cách chọn phương tiện đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt?
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:

Hỏi bạn Khoa có mấy cách chọn phương tiện đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt?
Câu 12:
Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận \(\overrightarrow n = \left( { - 2;\,\,7} \right)\) làm vectơ pháp tuyến là
Phương trình tổng quát của đường thẳng d đi qua điểm A(1; – 3) và nhận \(\overrightarrow n = \left( { - 2;\,\,7} \right)\) làm vectơ pháp tuyến là
Câu 13:
Nếu một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện, ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai, ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động số hai, có k cách thực hiện hành động số ba thì số cách hoàn thành công việc đó là
Nếu một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện, ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai, ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động số hai, có k cách thực hiện hành động số ba thì số cách hoàn thành công việc đó là
Câu 14:
Cho hai vectơ \(\overrightarrow x = \left( {3;\, - 4} \right)\), \(\overrightarrow y = \left( { - 6;\,\,8} \right)\). Khẳng định nào sau đây là đúng?
Cho hai vectơ \(\overrightarrow x = \left( {3;\, - 4} \right)\), \(\overrightarrow y = \left( { - 6;\,\,8} \right)\). Khẳng định nào sau đây là đúng?
Câu 15:
Trong mặt phẳng tọa độ Oxy, cho A(2; 7) và B(– 2; 8). Độ dài đoạn thẳng AB là
Trong mặt phẳng tọa độ Oxy, cho A(2; 7) và B(– 2; 8). Độ dài đoạn thẳng AB là


