Một người đứng ở vị trí A trên nóc của một ngôi nhà cao 4m đang quan sát một cây cao

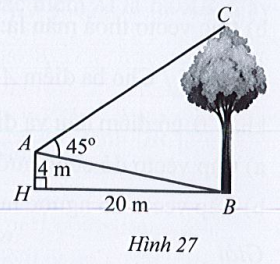
Bài 21 trang 81 SBT Toán 10 Tập 1: Một người đứng ở vị trí A trên nóc của một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20 m và đo được $\widehat{BAC}=45°$(Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

Trả lời

Xét tám giác vuông AHB, có:

AB² = AH² + HB² (định lí pythagoras)

⇔ AB² = 4² + 20²

⇔ AB² = 416

⇔ AB ≈ 20,4

Ta lại có: $\tan \widehat{HAB}=\frac{HB}{HA}$ ⇔ $\tan \widehat{HAB}=\frac{20}{4}=5$$\Rightarrow \widehat{HAB}\approx 78,7°$

Ta có: AH ⊥ BH và CB ⊥ BH nên AH // CB

⇒ $\widehat{HAB}=\widehat{ABC}\approx 78,7°$ (hai góc so le trong)

Xét tam giác ABC có:

$$\begin{gathered} \widehat{C}=180°-\widehat{BAC}-\widehat{ABC} \\ =180°-45°-78,7°=56,3^o \end{gathered}$$

Áp dụng định lí sin trong tam giác ta được:

$\frac{BC}{\sin A}=\frac{AB}{\sin C}$

⇔ $BC=\frac{AB\sin A}{\sin C}=\frac{20,4.\sin 45°}{\sin 56,3°}\approx 17,3$.

Vậy chiều cao của cây là 17,3 m.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài ôn tập chương 3

Bài 1: Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180°

Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 3: Khái niệm vectơ

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ