Câu hỏi:
19/01/2024 87
Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,...
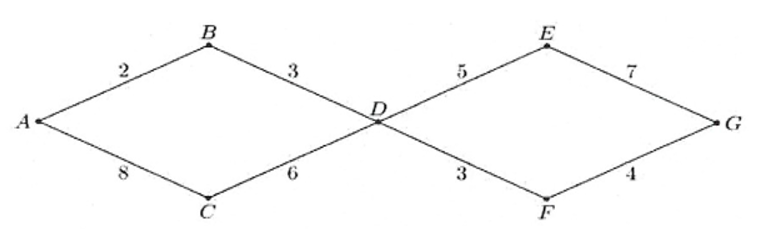
Số con đường từ A đến G là:
Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,...

Số con đường từ A đến G là:
A. 101;
A. 101;
B. 2 538;
B. 2 538;
C. 38;
D. 1 462.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta thấy để đi từ A đến G, ta bắt buộc phải đi qua D.
Bước 1: Đi từ A đến D.
• Phương án 1: Đi từ A, qua B, đến D thì có 2.3 = 6 con đường.
• Phương án 2: Đi từ A, qua C, đến D thì có 8.6 = 48 con đường.
Theo quy tắc cộng, ta có số cách đi từ A đến D là 6 + 48 = 54 con đường.
Bước 2: Đi từ D đến G.
• Phương án 1: Đi từ D, qua E, đến G thì có 5.7 = 35 con đường.
• Phương án 2: Đi từ D, qua F, đến G thì có 3.4 = 12 con đường.
Theo quy tắc cộng, ta có số cách đi từ D đến G là 35 + 12 = 47 con đường.
Vậy theo quy tắc nhân, ta có số cách đi từ A đến G là 54.47 = 2 538 con đường.
Do đó ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: D
Ta thấy để đi từ A đến G, ta bắt buộc phải đi qua D.
Bước 1: Đi từ A đến D.
• Phương án 1: Đi từ A, qua B, đến D thì có 2.3 = 6 con đường.
• Phương án 2: Đi từ A, qua C, đến D thì có 8.6 = 48 con đường.
Theo quy tắc cộng, ta có số cách đi từ A đến D là 6 + 48 = 54 con đường.
Bước 2: Đi từ D đến G.
• Phương án 1: Đi từ D, qua E, đến G thì có 5.7 = 35 con đường.
• Phương án 2: Đi từ D, qua F, đến G thì có 3.4 = 12 con đường.
Theo quy tắc cộng, ta có số cách đi từ D đến G là 35 + 12 = 47 con đường.
Vậy theo quy tắc nhân, ta có số cách đi từ A đến G là 54.47 = 2 538 con đường.
Do đó ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
Câu 2:
Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 2 viên bi. Có bao nhiêu cách lấy được 2 viên bi cùng màu?
Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 2 viên bi. Có bao nhiêu cách lấy được 2 viên bi cùng màu?
Câu 3:
Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất (một cây bút chì hoặc một cây bút bi hoặc một cuốn tập) thì số cách chọn khác nhau là:
Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất (một cây bút chì hoặc một cây bút bi hoặc một cuốn tập) thì số cách chọn khác nhau là:
Câu 4:
Có ba môn thi Toán, Vật lí, Hóa học cần xếp vào 3 buổi thi, mỗi buổi một môn sao cho môn Toán không thi buổi đầu thì số cách xếp là:
Có ba môn thi Toán, Vật lí, Hóa học cần xếp vào 3 buổi thi, mỗi buổi một môn sao cho môn Toán không thi buổi đầu thì số cách xếp là:
Câu 5:
Có bao nhiêu cách chọn và sắp xếp thứ tự 5 cầu thủ để đá luân lưu, biết rằng cả 11 cầu thủ đều có khả năng như nhau?
Có bao nhiêu cách chọn và sắp xếp thứ tự 5 cầu thủ để đá luân lưu, biết rằng cả 11 cầu thủ đều có khả năng như nhau?
Câu 6:
Cho x là số thực dương. Khai triển nhị thức , ta có hệ số của số hạng chứa xm bằng 6. Giá trị của m là:
Cho x là số thực dương. Khai triển nhị thức , ta có hệ số của số hạng chứa xm bằng 6. Giá trị của m là:
Câu 7:
Hội đồng quản trị của công ty X gồm 10 người. Hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí, biết khả năng mỗi người là như nhau.
Hội đồng quản trị của công ty X gồm 10 người. Hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí, biết khả năng mỗi người là như nhau.
Câu 8:
Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:
Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:
Câu 9:
Biết rằng trong khai triển (với x ≠ 0), hệ số của số hạng chứa là 640. Khi đó giá trị của a bằng:
Biết rằng trong khai triển (với x ≠ 0), hệ số của số hạng chứa là 640. Khi đó giá trị của a bằng:
Câu 13:
Từ các chữ số 1; 5; 6; 7; 9 có thể lập được bao nhiêu số tự nhiên có 4 chữ số?
Từ các chữ số 1; 5; 6; 7; 9 có thể lập được bao nhiêu số tự nhiên có 4 chữ số?
Câu 14:
Số hạng không chứa x trong khai triển (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:
Số hạng không chứa x trong khai triển (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:


