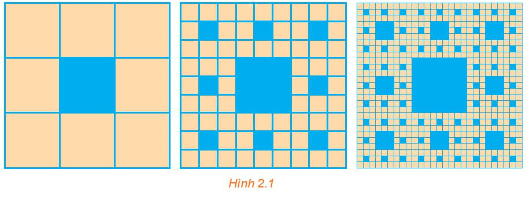
Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia th

Trả lời

Lời giải:

+ Chia lần 1: Hình vuông màu vàng lớn có cạnh bằng 1 đơn vị thì có diện tích bằng 1 (đvdt). Chia hình vuông này thành 9 hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh, thì hình vuông màu xanh đầu tiên này có diện tích bằng \(\frac{1}{9}\) (đvdt).

+ Chia lần 2: 8 hình vuông màu vàng còn lại, mỗi hình vuông này lại được chia thành 9 hình vuông con và tiếp tục tô xanh hình vuông chính giữa, khi đó mỗi hình vuông xanh nhỏ hơn có diện tích S₁ = \(\frac{1}{9} \cdot \frac{1}{9} = \frac{1}{{{9^2}}}\), 8 hình vuông xanh nhỏ hơn có diện tích bằng 8S₁.

Cứ tiếp tục như vậy, mỗi lần chia ta sẽ tạo thành 8 hình vuông xanh nhỏ hơn tiếp đối với mỗi ô vuông vàng nhỏ.

Do đó, quá trình này được tiếp tục lặp lại năm lần, thì trừ lần đầu tiên, 4 lần sau, mỗi lần chia diện tích ô vuông xanh tạo thành lập thành một cấp số nhân có u₁ = \(8.\frac{1}{{{9^2}}}\) và công bội \(q = 8.\frac{1}{9}\).

Vậy tổng diện tích các hình vuông được tô màu xanh là

S = \(\frac{1}{9} + \frac{{8.\frac{1}{{{9^2}}}\left( {1 - {{\left( {\frac{8}{9}} \right)}^4}} \right)}}{{1 - \frac{8}{9}}} = \frac{{26\,\,281}}{{59\,\,049}}\) (đvdt).