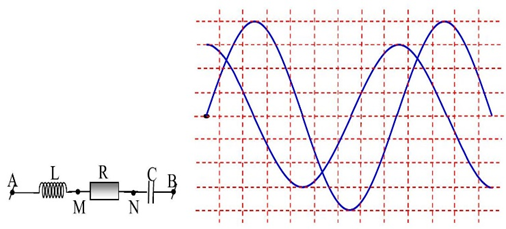
Một đoạn mạch AB chứa các phần tủ L, R và C như hình vẽ. Cuộn cảm thuần
27
19/07/2024
Một đoạn mạch \({\rm{AB}}\) chứa các phần tử \({\rm{L}},{\rm{R}}\) và \({\rm{C}}\) như hình vẽ. Cuộn cảm thuần có độ tự cảm \({\rm{L}}\), tụ điện có điện dung \({\rm{C}}\) và điện trở thuần \({\rm{R}} = 30{\rm{\Omega }}\). Đặt vào hai đầu \(AB\) một điện áp có biểu thức \(u = {U_0}{\rm{cos}}100\pi t\;\left( V \right)\), rồi dùng dao động kí điện tử để hiển thị đồng thời đồ thị điện áp giữa hai đầu đoạn mạch \({\rm{AN}}\) và MB ta thu được các đồ thị như hình vẽ bên. Các phần tử L và \(C\) có giá trị là.
A. \(C = \frac{{{{10}^{ - 4}}}}{{4\pi }}F;L = \frac{9}{{4\pi }}H\).
B. \(C = \frac{{{{10}^{ - 3}}}}{{4\pi }}F;L = \frac{9}{{4\pi }}H\).
C. \(C = \frac{{{{10}^{ - 4}}}}{{4\pi }}F;L = \frac{9}{{40\pi }}H\).
D. \(C = \frac{{{{10}^{ - 3}}}}{{4\pi }}F;L = \frac{9}{{40\pi }}H\).
Trả lời
\(\frac{{{U_{AN}}}}{{{U_{MB}}}} = \frac{{{Z_{AN}}}}{{{Z_{MB}}}} = \frac{3}{4} \Rightarrow \left\{ \begin{array}{l}{Z_{AN}} = 3x\\{Z_{MB}} = 4x\end{array} \right.\)
\({u_{AN}}\) sớm pha \(\pi /2\;\) so với \({u_{MB}}\)
\( \Rightarrow {\cos ^2}{\varphi _{AN}} + {\cos ^2}{\varphi _{MB}} = 1 \Rightarrow {\left( {\frac{R}{{{Z_{AN}}}}} \right)^2} + {\left( {\frac{R}{{{Z_{MB}}}}} \right)^2} = 1 \Rightarrow {\left( {\frac{{30}}{{3x}}} \right)^2} + {\left( {\frac{{30}}{{4x}}} \right)^2} = 1 \Rightarrow x = 12,5\)
\({Z_C} = \sqrt {Z_{MB}^2 - {R^2}} = \sqrt {{{\left( {4.12,5} \right)}^2} - {{30}^2}} = 40\Omega \to C = \frac{1}{{\omega {Z_C}}} = \frac{1}{{100\pi .40}} = \frac{{{{10}^{ - 3}}}}{{4\pi }}F\)
\({Z_L} = \sqrt {Z_{AN}^2 - {R^2}} = \sqrt {{{\left( {3.12,5} \right)}^2} - {{30}^2}} = 22,5\Omega \to L = \frac{{{Z_L}}}{\omega } = \frac{{22,5}}{{100\pi }} = \frac{9}{{40\pi }}H\). Chọn D