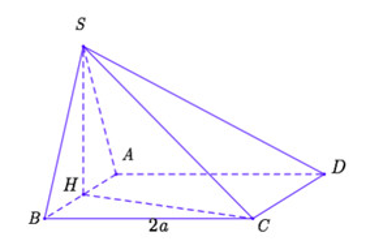
ho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy.

Trả lời

Gọi H là trung điểm của AB

Þ SH ⊥ AB (do ΔSAB cân tại S)

Ta có: (SAB) ⊥ (ABCD)

(SAB) ∩ (ABCD) = AB

SH ⊥ AB; SH ⊂ (SAB)

Þ SH ⊥ (ABCD)

Hay H là hình chiếu của S lên mặt phẳng (ABCD)

Þ CH là hình chiếu của SC lên mặt phẳng (ABCD)

Do đó góc giữa SC và mặt đáy là  $\widehat{SCH}=\alpha$.

Ta có:  $V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}$

 $\iff \frac{4a^3}{3}=\frac{1}{3}SH.4a^2\iff SH=a$

Xét tam giác BHC vuông tại B, theo định lý Pytago ta có:

 $HC=\sqrt{B{H}^2+B{C}^2}=\sqrt{a^2+4a^2}=a\sqrt{5}$

Xét tam giác SHC vuông tại H có:

 $\tan \widehat{SCH}=\frac{SH}{HC}=\frac{a}{a\sqrt{5}}=\frac{1}{\sqrt{5}}$

Vậy  $\tan \widehat{SCH}=\frac{1}{\sqrt{5}}$.