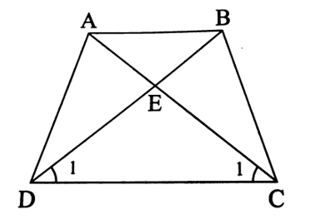
Gọi E là giao điểm của AC và BD.

Trong ∆ECD, ta có ${\widehat{C}}_1=\widehat{D_1}$ nên ∆ECD cân tại E, suy ra EC = ED. (1)

Ta có: AB // CD nên

⦁ $\widehat{\text{EBA}}=\widehat{D_1}$ (hai góc so le trong);

⦁ $\widehat{\text{EAB}}=\widehat{C_1}$ (hai góc so le trong);

⦁ ${\widehat{C}}_1=\widehat{D_1}$ (giả thiết).

Suy ra $\widehat{\text{EBA}}=\widehat{\text{EAB}}$, do đó ∆BEA cân tại E.

Nên AE = BE. (2)

Ta có: AC = AE + EC; BD = BE + ED (3)

Từ (1), (2) và (3) suy ra AC = BD.

Hình thang ABCD có hai đường chéo bằng nhau nên ABCD là hình thang cân.