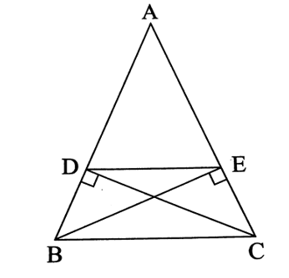
Do BE, CD là hai đường cao nên BE ⊥ AC, CD ⊥ AB.

Xét ∆BEC vuông tại E và ∆CDB vuông tại D, ta có:

BC là cạnh chung; $\widehat{\text{ECB}}=\widehat{\text{DBC}}$ (do ∆ABC cân tại A)

Do đó ∆BEC = ∆CDB (cạnh huyền – góc nhọn)

Suy ra EC = BD (hai cạnh tương ứng)

Mà AC = AB nên AC ‒ EC = AB ‒ BD, hay AE = AD

Do đó ∆ADE cân tại A suy ra $\widehat{\text{ADE}}=\widehat{\text{AED}}=\frac{180°-\widehat{A}}{2}.$ (1)

Vì ∆ABC cân tại A nên $\widehat{\text{ABC}}=\widehat{\text{ACB}}=\frac{180°-\widehat{A}}{2}.$ (2)

Từ (1) và (2) suy ra $\widehat{\text{ADE}}=\widehat{\text{ABC}}$

Mà hai góc này ở vị trí đồng vị nên DE // BC

Suy ra tứ giác BDEC là hình thang.

Hình thang BDEC có $\widehat{DBC}=\widehat{ECB}$ nên là hình thang cân.