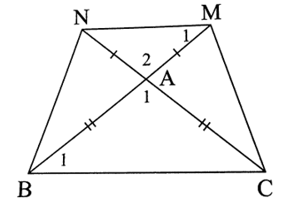
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho AM = AN. Chứng minh tứ giác MNBC là hình thang cân.
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho AM = AN. Chứng minh tứ giác MNBC là hình thang cân.