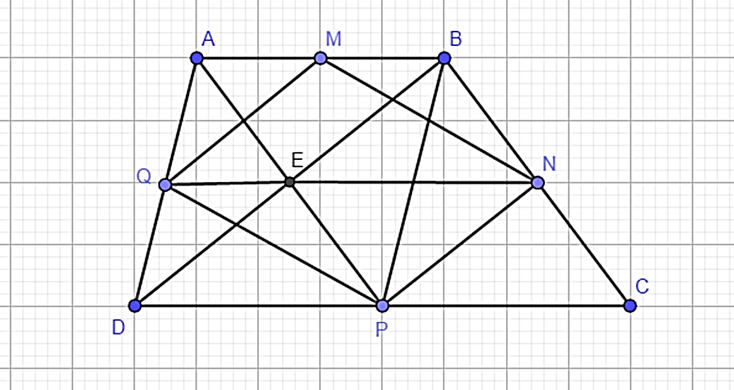
a) Do DC = 2AB mà P là trung điểm DC nên AB = DP = PC
Tứ giác ABPD có AB // DP và AB = DP nên ABPD là hình bình hành
M, N, P, Q thứ tự là trung điểm các cạnh AB, BC, CD, DA nên ta có:
MQ là đường trung bình trong tam giác ABD nên MQ // BD và MQ = \(\frac{1}{2}\)BD
NP là đường trung bình trong tam giác CBD nên NP // BD và NP = \(\frac{1}{2}\)BD
Suy ra tứ giác MNPQ có NP // MQ và NP = MQ nên MNPQ là hình bình hành.
b) Để MNPQ là hình thoi thì MQ = MN ⇔ \(\frac{1}{2}\)BD = \(\frac{1}{2}\)AC ⇔ AC = BD
Suy ra ABCD là hình thang cân thì MNPQ là hình thoi
c) ABPD là hình bình hành nên E là giao điểm của BD và AP thì E là trung điểm của BD
QE là đường trung bình trong tam giác DAB nên QE // AB
EN là đường trung bình trong tam giác BCD nên EN // DC
Mà AB // DC nên Q, E, N thẳng hàng.