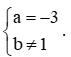Hãy xác định hàm số y = ax + b trong mỗi trường hợp sau: Đồ thị của hàm số là đường thẳng đi qua điểm B(–1; 2) và cắt trục tung tại điểm có tung độ bằng 3

Bài 6 trang 17 SBT Toán 8 Tập 2: Hãy xác định hàm số y = ax + b trong mỗi trường hợp sau:

a) Đồ thị của hàm số là đường thẳng đi qua điểm B(–1; 2) và cắt trục tung tại điểm có tung độ bằng 3.

b) Đồ thị của hàm số là đường thẳng song song với đường thẳng y = –3x + 1 và cắt trục hoành tại điểm có hoành độ bằng 3.

c) Đồ thị của hàm số là đường thẳng cắt trục tung tại điểm có tung độ bằng –6 và cắt trục hoành tại điểm có hoành độ bằng 2.

Trả lời

a) Đồ thị của hàm số y = ax + b đi qua điểm B(–1; 2).

•Thay B(–1; 2) vào y = ax + b, ta được:

2 = –1.a + b $\iff$ b – a = 2 (1)

Đồ thị của hàm số y = ax + b cắt trục tung tại điểm M có tung độ bằng 3 hay M(0; 3).

•Thay M(0; 3) vào y = ax + b, ta được:

3 = a.0 + b $\iff$ b = 3

•Thay b = 3 vào (1) ta có:

3 – a = 2 $\iff$ a = 1

Vậy hàm số cần tìm có phương trình y = x + 3.

b) Đồ thị của hàm số y = ax + b song song với đường thẳng y = –3x + 1 nên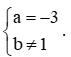 

Đồ thị của hàm số y = ax + b cắt trục hoành tại điểm N có hoành độ bằng 3 nên N(3; 0).

•Thay N(3; 0) vào y = ax + b ta được: 3a + b = 0.

•Thay a = –3 vào ta có: 3.(–3) + b = 0 $\iff$ b = 9 (TMĐK).

Vậy hàm số cần tìm có phương trình y = –3x + 9.

c) Đồ thị của hàm số y = ax + b cắt trục tung tại điểm P có tung độ bằng – 6 hay P(0; –6).

Thay P(0; –6) vào y = ax + b ta được: 3.0 + b = –6 $\iff$ b = –6.

Đồ thị của hàm số y = ax + b cắt trục hoành tại điểm Q có hoành độ bằng 2 hay Q(2; 0).

Thay Q(2; 0) vào y = ax + b ta được: 2a + b = 0.

Mà b = –6 nên 2a – 6 = 0 $\iff$ a = 3.

Vậy hàm số cần tìm có phương trình y = 3x – 6.

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tọa độ của một điểm và đồ thị của hàm số

Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 4: Hệ số góc của đường thẳng

Bài tập cuối chương 5

Bài 1: Phương trình bậc nhất một ẩn

Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất