Câu hỏi:
19/01/2024 49Hai tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 120°. Tàu 1 chạy với vận tốc 30 hải lí/giờ. Tàu 2 chạy với vận tốc 25 hải lí/giờ. Sau hai giờ, hai tàu cách nhau khoảng:
A. 47,7 hải lí;
B. 95,4 hải lí;
C. 2275 hải lí;
D. 9100 hải lí.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
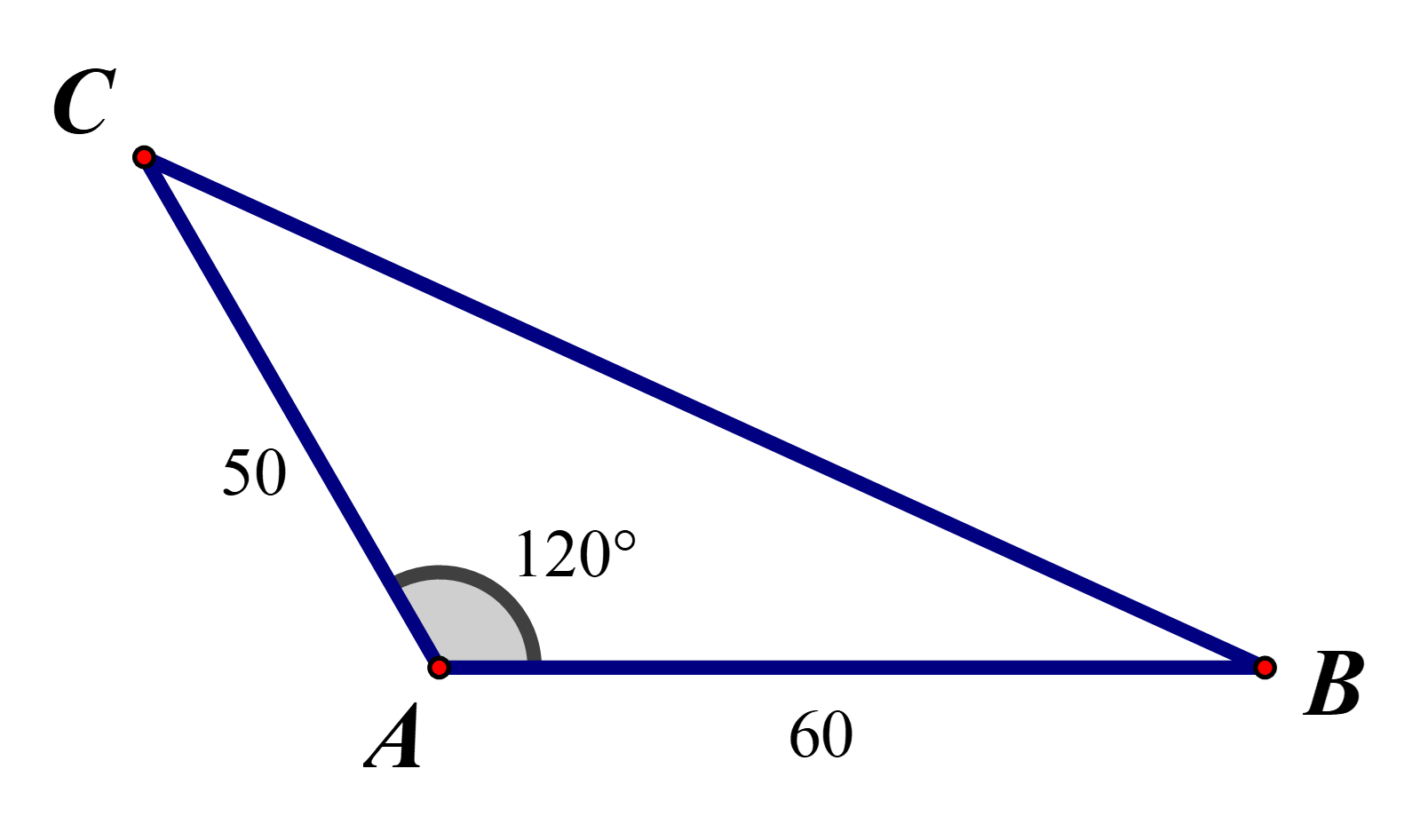
Giả sử sau hai giờ, tàu 1 đến vị trí điểm B, tàu 2 đến vị trí điểm C.
Sau hai giờ, tàu 1 đi được 2.30 = 60 (hải lí).
Suy ra AB = 60.
Sau hai giờ, tàu hai đi được 2.25 = 50 (hải lí).
Suy ra AC = 50.
Ta có BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 602 + 502 – 2.60.50.cos120°
= 9100
Suy ra BC = \(\sqrt {9100} = 10\sqrt {91} \approx 95,4\).
Vì vậy sau hai giờ, hai tàu cách nhau khoảng 95,4 hải lí.
Vậy ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: B

Giả sử sau hai giờ, tàu 1 đến vị trí điểm B, tàu 2 đến vị trí điểm C.
Sau hai giờ, tàu 1 đi được 2.30 = 60 (hải lí).
Suy ra AB = 60.
Sau hai giờ, tàu hai đi được 2.25 = 50 (hải lí).
Suy ra AC = 50.
Ta có BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 602 + 502 – 2.60.50.cos120°
= 9100
Suy ra BC = \(\sqrt {9100} = 10\sqrt {91} \approx 95,4\).
Vì vậy sau hai giờ, hai tàu cách nhau khoảng 95,4 hải lí.
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
∆ABC có \(AB = \frac{{\sqrt 6 - \sqrt 2 }}{2}\), \(BC = \sqrt 3 \), \(CA = \sqrt 2 \). Gọi D là chân đường phân giác trong của \(\widehat A\). Khi đó số đo của \(\widehat {ADB}\) bằng:
Câu 2:
Cho ∆ABC và các khẳng định sau:
(I) b2 – c2 = a(b.cosC – c.cosB);
(II) (b + c)sinA = a(sinB + sinC);
(III) ha = 2R.sinB.sinC;
(IV) S = R.r.(sinA + sinB + sin C);
Số khẳng định đúng là:
Câu 3:
Cho ∆ABC. Nếu tăng cạnh AB lên 4 lần và tăng cạnh AC lên 5 lần và giữ nguyên độ lớn của \(\widehat A\) thì khi đó diện tích của tam giác mới S’ được tạo nên bằng:
Câu 4:
∆ABC vuông cân tại A và nội tiếp đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp ∆ABC. Khi đó tỉ số \(\frac{R}{r}\) bằng:


