Bài 3.21 trang 39 SBT Toán 8 Tập 1: Hai đường trung tuyến BM, CN của tam giác ABC cân tại A cắt nhau tại G. Gọi H, K lần lượt là điểm sao cho trung điểm của GH là M, trung điểm của GK là N. Chứng minh tứ giác BCHK là hình chữ nhật.
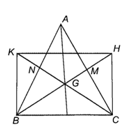
Vì BM, CN là trung tuyến của ∆ABC nên M, N lần lượt là trung điểm của AC, AB.
Do M là trung điểm của AC và của GH nên AGCH là hình bình hành
Từ đó HC = AG và HC // AG. (1)
Do N là trung điểm của AB và của GK nên AGBK là hình bình hành
Suy ra KB = AG và KB // AG. (2)
Từ (1) và (2) suy ra BK = CH và BK // CH.
Tứ giác BCHK có hai cạnh đối BK, CH bằng nhau và song song nên là một hình bình hành.
Vì tam giác ABC cân tại A nên trung tuyến AG là đường cao tức AG ⊥ BC hay KB ⊥ BC, suy ra BCHK là hình chữ nhật.
Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác: