Gọi O là tâm của hình bát giác đều ABCDEFGH. a) Tìm hai vectơ khác
Bài 6 trang 91 SBT Toán 10 Tập 1: Gọi O là tâm của hình bát giác đều ABCDEFGH.
a) Tìm hai vectơ khác →0 và cùng hướng với →OA.
b) Tìm vectơ bằng vectơ →BD.
Bài 6 trang 91 SBT Toán 10 Tập 1: Gọi O là tâm của hình bát giác đều ABCDEFGH.
a) Tìm hai vectơ khác →0 và cùng hướng với →OA.
b) Tìm vectơ bằng vectơ →BD.
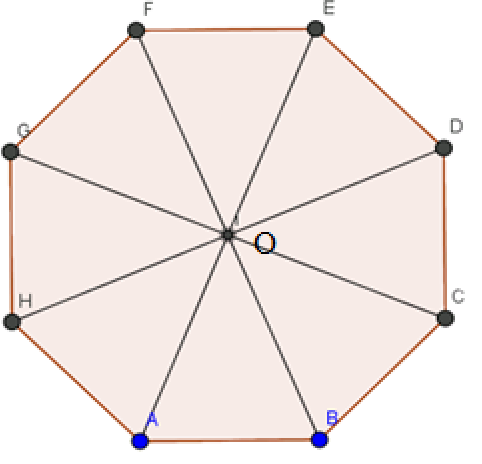
a) Hai vectơ khác →0 và cùng hướng với →OA: →EO, →EA.
b) Ta có: ^DOB=28.360°⇒ DH vuông góc với FB.
Xét tứ giác FDBH: Hai đường chéo DH và FB vuông góc với nhau tại O là trung điểm của mỗi đường nên FDBH là hình thoi. ( DHNB hình thoi )
Lại có FB = DH ( do đều là đường chéo của bát giác đều ) nên FDBH là hình vuông. (DHNB hình vuông )
⇒ HF = BD và HF // BD.
Như vậy ta có vectơ bằng vectơ là .
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Định lí côsin và định lí sin
Bài 2: Tổng và hiệu của hai vectơ