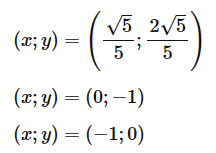Giải hệ phương trình: x^2 + x - xy - 2y^2}- 2y = 0; x^2 + y^2 = 1

Trả lời

Lời giải

Ta có:

\({x^2} + x - xy - 2{y^2} - 2xy = 0\)

\( \Leftrightarrow {x^2} - 2xy + xy - 2{y^2} + x - 2y = 0\)

\( \Leftrightarrow x(x - 2y) + y(x - 2y) + (x - 2y) = 0\)

\( \Leftrightarrow (x + y + 1)(x - 2y) = 0\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + y + 1 = 0}\\{x - 2y = 0}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + y = - 1}\\{x = 2y}\end{array}} \right.\)

Thay x = 2y vào phương trình x² + y² = 1 ta có:

\(4{y^2} + {y^2} = 1\)

\( \Leftrightarrow 5{y^2} = 1\)

\( \Leftrightarrow {y^2} = \frac{1}{5}\)

\( \Leftrightarrow y = \frac{{\sqrt 5 }}{5}\)

\( \Rightarrow x = 2 \cdot \frac{{\sqrt 5 }}{5} = \frac{{2\sqrt 5 }}{5}\)

Ta có \(x + y = - 1\)

\( \Leftrightarrow {(x + y)^2} - 2xy = 1\)

\( \Leftrightarrow 1 - 2xy = 1\)

\( \Leftrightarrow xy = 0\)

Lại có x + y = –1

Do đó x = –1 – y

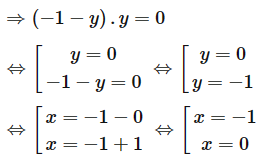
Vậy nghiệm của hệ phương trình là: