Câu hỏi:
19/12/2023 101
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn bao nhiêu mét ? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau: \(\left\{ \begin{array}{l}x = {v_o}t\\y = h - \frac{1}{2}g{t^2}\end{array} \right.\)
trong đó, v0 là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn bao nhiêu mét ? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau: \(\left\{ \begin{array}{l}x = {v_o}t\\y = h - \frac{1}{2}g{t^2}\end{array} \right.\)
trong đó, v0 là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.

A. \(\frac{{50\sqrt {10} }}{{9,8}}\) m;
B. \(\frac{{100\sqrt {10} }}{{9,8}}\)m;
C. \(\frac{{200\sqrt {10} }}{{9,8}}\)m;
D. \(\frac{{20\sqrt {10} }}{{9,8}}\)m.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C.
Theo đề bài, ta có biểu thức tọa độ của thùng hàng: \(\left\{ \begin{array}{l}x = 50t\\y = 80 - \frac{1}{2}g{t^2}\end{array} \right.\).
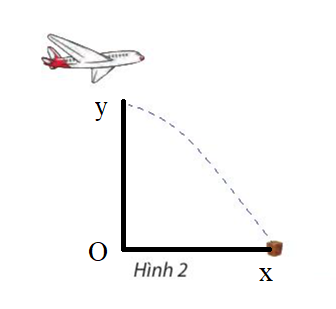
Đặt hệ trục tọa độ như hình vẽ. Khi thùng hàng rơi đúng vị trí, ta có:
y = 0 \( \Leftrightarrow 80 - \frac{1}{2}g{t^2} = 0 \Leftrightarrow \frac{1}{2}g{t^2} = 80 \Leftrightarrow g{t^2} = 160 \Leftrightarrow {t^2} = \frac{{160}}{g} \Leftrightarrow t = \frac{{\sqrt {160} }}{g}\)
Khi đó, ta có: \(x = 50.\frac{{\sqrt {160} }}{g} = \frac{{200\sqrt {10} }}{{9,8}}\) (m)
Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn \(\frac{{200\sqrt {10} }}{{9,8}}\) m.
Hướng dẫn giải:
Đáp án đúng là: C.
Theo đề bài, ta có biểu thức tọa độ của thùng hàng: \(\left\{ \begin{array}{l}x = 50t\\y = 80 - \frac{1}{2}g{t^2}\end{array} \right.\).

Đặt hệ trục tọa độ như hình vẽ. Khi thùng hàng rơi đúng vị trí, ta có:
y = 0 \( \Leftrightarrow 80 - \frac{1}{2}g{t^2} = 0 \Leftrightarrow \frac{1}{2}g{t^2} = 80 \Leftrightarrow g{t^2} = 160 \Leftrightarrow {t^2} = \frac{{160}}{g} \Leftrightarrow t = \frac{{\sqrt {160} }}{g}\)
Khi đó, ta có: \(x = 50.\frac{{\sqrt {160} }}{g} = \frac{{200\sqrt {10} }}{{9,8}}\) (m)
Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn \(\frac{{200\sqrt {10} }}{{9,8}}\) m.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe mới với chi phí mua vào một chiếc là 27 triệu đồng và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá lợi nhuận thu được sẽ là cao nhất.
Câu 2:
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất (giống bài toán tầm bay cao, tầm bay xa). Biết quỹ đạo của quả bóng là một parabol trong trục tọa độ Oth với t là thời gian, h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2 m. Sau 1 giây, nó đạt độ cao 8,5 m và 2 giây sau nó ở độ cao 6 m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t.
Câu 3:
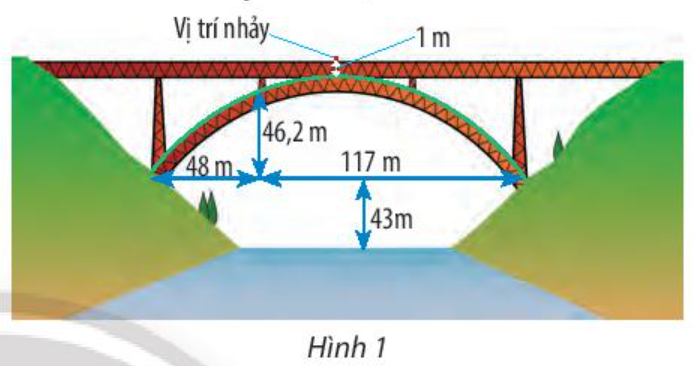
Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước). Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người muốn thực hiện một cú nhảy bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu ? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.

Câu 4:
Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.
Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:
– Dây dài nhất là 5m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.
– Nhịp cầu dài 30 m.
– Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.
Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:
– Dây dài nhất là 5m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.
– Nhịp cầu dài 30 m.
– Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Câu 5:
Một người chơi cầu lông có khuynh hướng phát cầu với góc 30° (so với mặt đất). Hãy tính khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa), biết cầu rời mặt vợt ở độ cao 0,7 m so với mặt đất và vận tốc ban đầu của cầu là 12 m/s (bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng).
Câu 6:
Một chiếc cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\). Biết cổng có chiều rộng d = 5 mét. Hãy tính chiều cao h của cổng.


Câu 7:
Một cửa hàng buôn giày nhập một đôi với giá là 40 đô. Cửa hàng ước tính rằng nếu đôi giày bán được với giá x đô thì mỗi tháng khách hàng sẽ mua 120 – x đôi giày. Hỏi cửa hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất.
Câu 8:
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng P(n) = 360 – 10n. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lượng cá sau một vụ thu được nhiều nhất ?
Câu 9:
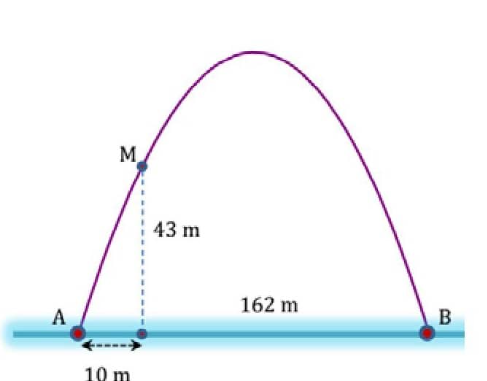
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất, người ta thả một sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch.

Câu 10:
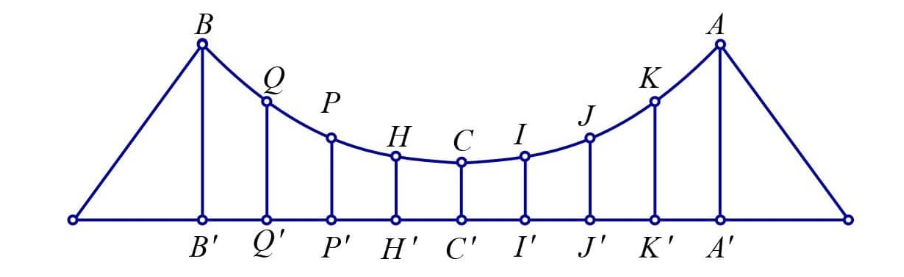
Dây truyền đỡ trên cầu treo có dạng Parabol ACB như hình vẽ. Đầu, cuối của dây được gắn vào các điểm A, B trên mỗi trục AA’ và BB’ với độ cao 30 m. Chiều dài đoạn A’B’ trên nền cầu bằng 200 m. Độ cao ngắn nhất của dây chuyền trên cầu là OC = 5 m. Gọi Q’, P’, H’, O, I’, J’, K’ là các điểm chia đoạn A’B’ thành các phần bằng nhau. Các thanh thẳng đứng nối nền cầu với đáy dây chuyền: QQ’, PP’, HH’, OC, II, JJ’, KK’ gọi là các dây cáp treo. Tính tổng độ dài của các dây cáp treo ?