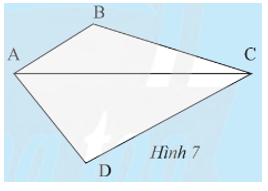
Đường chéo AC chia tứ giác ABCD thành hai tam giác ACB và ACD (Hình 7). Tính tổng các góc của tam giác ACB và tam giác ACD. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác ABCD?

• Xét DACB có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (định lí tổng ba góc trong một tam giác).

Xét DACD có: $\widehat{CAD}+\widehat{ACD}+\widehat{ADC}=180°$ (định lí tổng ba góc trong một tam giác).

Do đó $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}+\widehat{CAD}+\widehat{ACD}+\widehat{ADC}=180°+180°=360°$.

Vậy tổng các góc của tam giác ACB và tam giác ACD bằng 360°.

• Ta có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}+\widehat{CAD}+\widehat{ACD}+\widehat{ADC}=360°$

Suy ra $\left(\widehat{BAC}+\widehat{CAD}\right)+\widehat{ABC}+\left(\widehat{ACB}+\widehat{ACD}\right)+\widehat{ADC}=360°$

Hay $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$.

Vậy tổng các góc của tứ giác ABCD bằng 360°.