Chứng minh tứ giác OEAF là hình chữ nhật và DB^2= DA.DC
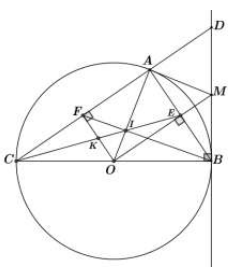
Cho đường tròn tâm O đường kính BC, lấy điểm A bất kỳ trên đường tròn (O) (A khác B và C). Kẻ OE⊥AB tại E và kẻ OF⊥AC tại F, tiếp tuyến tại B của đường tròn cắt CA tại D. Tia OE cắt BD tại M. Gọi I là giao điểm của BF và AO, gọi K là giao điểm của IC và OF.
Chứng minh tứ giác OEAF là hình chữ nhật và DB2=DA.DC .