Cho đường tròn $\left(O;R\right),$  đường kính $AB.$  Qua A vẽ đường thẳng d là tiếp tuyến của đường tròn $\left(O;R\right).$ C là một điểm thuộc đường thẳng d. Qua C vẽ tiếp tuyến thứ hai của đường tròn $\left(O;R\right).$  tiếp xúc với đường tròn $\left(O;R\right)$  tại điểm M. Gọi H là giao điểm của AM và OC

Chứng minh AM vuông góc với OC và $OH.OC=R^2.$

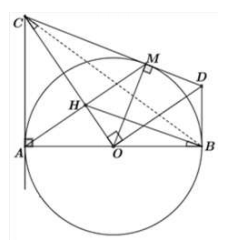
Theo giả thiết ta có hai đường tiếp tuyến tại A và M của đường tròn $\left(O\right)$  cặt nhau tại C

 $\Rightarrow OC$ là tia phân giác của $\angle ACM$  và $\angle AOM$  (tính chất hai tiếp tuyến cắt nhau).

Xét $\Delta AOM$  có: $OA=OM\left(=R\right)$  và có $OC$  là tia phân giác của $\angle AOM\left(cmt\right)$

$\Rightarrow OC$ đồng thời là đường cao của tam giác cân $AOM.$  (tính chất)

$\Rightarrow OC\perp AM=\left\{H\right\}$

Vậy $AM\perp OC.$

Áp dụng hệ thức lượng cho $\Delta OMC$  vuông tại M có đường cao OH có:

$OH.OC=O{M}^2\iff OH.OC=R^2.\left(dpcm\right)$

Vậy $OH.OC=R^2$