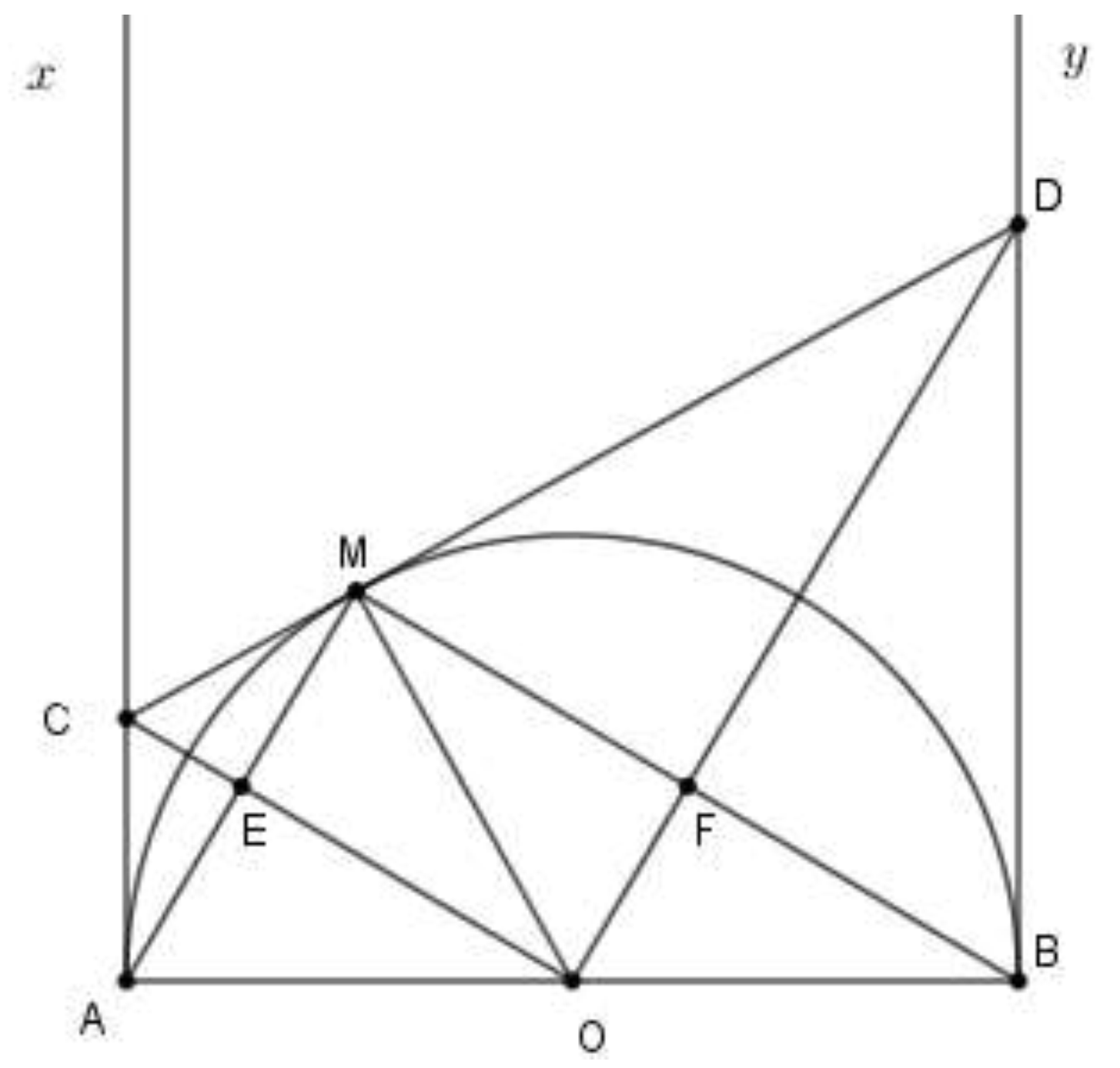
Chứng minh tích AC.BD không đổi khi M di động trên nửa đường tròn.
Cho nửa đường tròn tâm O, đường kính AB=2R . Trên nửa mặt phẳng có bờ là AB chứa nửa đường tròn, vẽ tiếp tuyến Ax, By. Từ điểm M tùy ý thuộc đường tròn (M khác A, B) vẽ tiếp tuyến tại M cắt Ax, By lần lượt tại C, D. Gọi E là giao điểm của CO và AM, F là giao điểm của DO và BM.
Chứng minh tích AC.BD không đổi khi M di động trên nửa đường tròn.