Chứng minh rằng ngũ giác có năm cạnh bằng nhau và ba góc liên tiếp bằng nhau
Chứng minh rằng ngũ giác có năm cạnh bằng nhau và ba góc liên tiếp bằng nhau là ngũ giác đều.
Chứng minh rằng ngũ giác có năm cạnh bằng nhau và ba góc liên tiếp bằng nhau là ngũ giác đều.
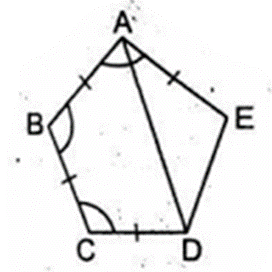
Xét tứ giác ABCD có \(\widehat B = \widehat C,AB = C{\rm{D}}\)
Suy ra ABCD là hình thang cân
Do đó \(\widehat {BA{\rm{D}}} = \widehat {C{\rm{D}}A}\) (1)
Vì AE = ED nên tam giác ADE cân tại E
Suy ra \(\widehat {E{\rm{AD}}} = \widehat {E{\rm{DA}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {BA{\rm{D}}} + \widehat {E{\rm{AD}}} = \widehat {C{\rm{D}}A} + \widehat {E{\rm{D}}A}\)
Hay \(\widehat {BA{\rm{E}}} = \widehat {C{\rm{D}}E}\)
Chứng minh tương tự với tứ giác ABCE ta được \(\widehat C = \widehat E\)
Do đó \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Vậy ngũ giác có năm cạnh bằng nhau và ba góc liên tiếp bằng nhau là ngũ giác đều.