Chứng minh MD=MA+BD và tam giác OMD vuông.
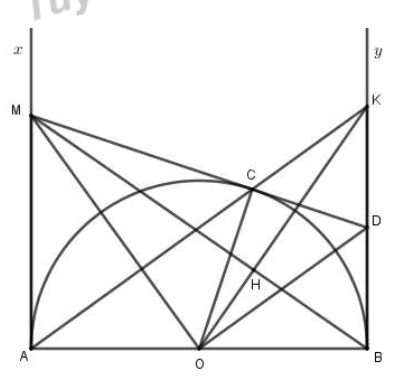
Cho nửa đường tròn (O;R) đường kính AB. Vẽ hai tiếp tuyến Ax, By với nửa đường tròn đó. Trên tia Ax lấy điểm M sao cho AM>R . Từ M kẻ tiếp tuyến MC với nửa đường tròn (O) (C là tiếp điểm). Tia MC cắt tia By tại D.
Chứng minh MD=MA+BD và tam giác OMD vuông.