Lời giải
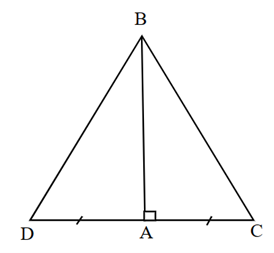
Trên tia đối của tia AC lấy điểm D sao cho AC = AD
Xét ∆ABC và ∆ABD có
AC = AD
\(\widehat {BAC} = \widehat {BA{\rm{D}}} = 90^\circ \)
AB là cạnh chung
Suy ra ∆ABC = ∆ABD (c.g.c)
Do đó \(\widehat {ABC} = \widehat {AB{\rm{D}}}\) (hai góc tương ứng), BC = BD (hai cạnh tương ứng)
Ta có \(AC = \frac{1}{2}BC\) (giả thiết)
AC = AD
Suy ra \(A{\rm{D}} = \frac{1}{2}BC\)
Do đó AC + AD = BC
Hay CD = BC
Mà BC = BD
Suy ra BC = BD = CD
Do đó tam giác BCD đều
Suy ra \(\widehat {DBC} = 60^\circ \)
Lại có \(\widehat {ABC} + \widehat {AB{\rm{D}}} = \widehat {CB{\rm{D}}}\), \(\widehat {ABC} = \widehat {AB{\rm{D}}}\) (chứng minh trên)
Do đó \(\widehat {ABC} = \widehat {AB{\rm{D}}} = \frac{{60^\circ }}{2} = 30^\circ \)
Vậy nếu trong tam giác vuông có 1 cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh ấy bằng 30°.