Chứng minh định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau"
390
14/11/2023
Luyện tập 2 trang 107 Toán lớp 7 Tập 1: Chứng minh định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.
Trả lời
Giả sử hai đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại hai điểm A và B.
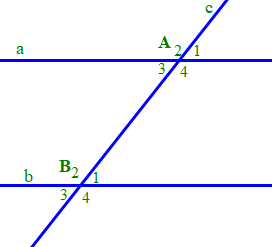
|
GT
|
c cắt a tại A, c cắt b tại B;
ˆA1=ˆB1.
|
|
KL
|
ˆA3=ˆB1, ˆA4=ˆB2
|
Ta có: ˆA1=ˆA3 (hai góc đối đỉnh)
ˆA1=ˆB1 (GT)
Suy ra ˆA3=ˆB1 (cùng bằng ˆA1).
Vì ^A3;^A4 là hai góc kề bù nên ^A3+^A4=180°
Do đó (1)
Lại có: là hai góc kề bù nên
Do đó (2)
Mà (chứng minh trên) (3)
Từ (1), (2) và (3) suy ra (hai góc so le trong).
Vậy ,
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài tập cuối chương 3
Bài 1: Góc ở vị trí đặc biệt
Bài 2: Tia phân giác của một góc
Bài 3: Hai đường thẳng song song
Bài 4: Định lí
Bài tập cuối chương 4

