Chứng minh các định lí sau: a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó
279
08/12/2023
Bài 3 trang 99 Toán 11 Tập 2: Chứng minh các định lí sau:
a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;
b) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai
mặt phẳng đó thì vuông góc với mặt phẳng còn lại.
Trả lời
a)
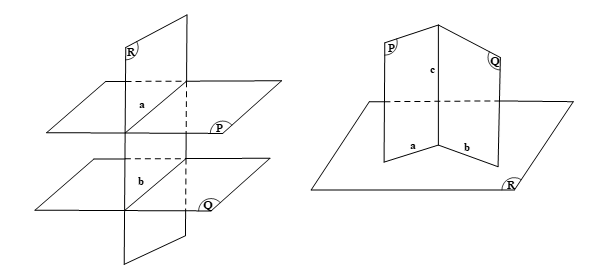
Giả sử ta có: (P) ⊥ (R), (Q) ⊥ (R), gọi a = (P) ∩ (R), b = (Q) ∩ (R).
Mà (P) và (Q) là hai mặt phẳng phân biệt nên a và b không trùng nhau.
Hơn nữa: a và b cùng nằm trong (R), nên xảy ra hai trường hợp:
⦁ Nếu a // b, mà a ⊂ (P), b ⊂ (Q) thì suy ra (P) // (Q).
⦁ Nếu a cắt b, mà a ⊂ (P) và b ⊂ (Q), thì ta gọi c = (P) ∩ (Q).
Do (P) ⊥ (R), (Q) ⊥ (R) và c = (P) ∩ (Q) nên suy ra c ⊥ (R).
b)
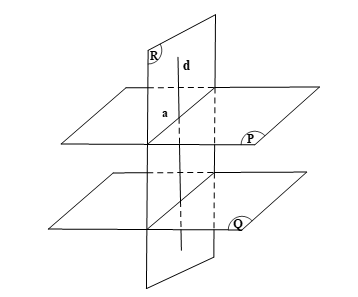
Giả sử có ba mặt phẳng (P), (Q), (R) thỏa mãn (P) // (Q) và (R) ⊥ (P). Ta cần chứng minh (R) ⊥ (Q).
Gọi a = (P) ∩ (R), lấy d ⊂ (R) sao cho a ⊥ d.
Ta có: (R) ⊥ (P), a = (R) ∩ (P), d ⊂ (R) và a ⊥ d, suy ra d ⊥ (P).
Mà (P) // (Q), d ⊂ (R) nên d ⊥ (Q).
Suy ra (Q) ⊥ (R).
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:


