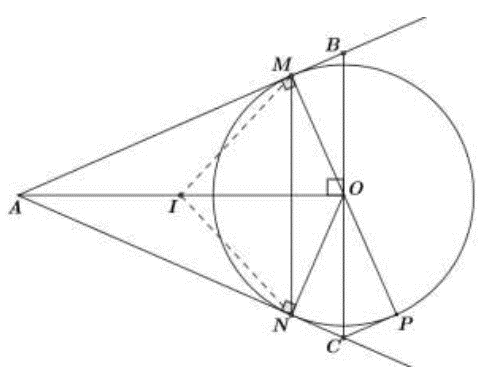
Từ điểm A nằm ngoài đường tròn $\left(O\right)$  ta kẻ hai tiếp tuyến AM và AN đến đường tròn (M và N là tiếp điểm). Đường thẳng MO cắt đường tròn tại điểm P. Đường thẳng vuông góc với OA tại O cắt AN tại C và cắt AM tại B.

Chứng minh bốn điểm A, M, O, N cùng thuộc một đường tròn.

Gọi I là trung điểm của AO.

Ta có: AM, AN là tiếp tuyến của đường tròn tại M và N.

$\Rightarrow \Delta AMO,\Delta ANO$ vuông tại M và N.

$\Rightarrow \left\{\begin{array}{l}IM=IA=IO=\frac{AO}{2}\\ IN=IA=IO=\frac{AO}{2}\end{array}\right.\left(t/c\right)\Rightarrow IM=IA=IN=IO\Rightarrow$A, M, O, N cùng thuộc đường tròn tâm I (t/c).

Vậy bốn điểm A, M, O, N cùng thuộc một đường tròn.