Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (O) ( B và C là 2 tiếp điểm)

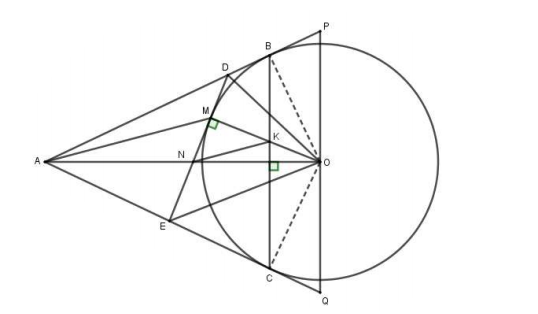
Gọi N là trung điểm của AO.

Tam giác AOB vuông tại B nên $BN=\frac{1}{2}AO=NA=NO\left(1\right)$

Tương tự ta có  $CN=\frac{1}{2}AO=NA=NO\left(2\right)$

Từ (1) và $\left(2\right)$  suy ra $NB=NA=NO=NC$ .

Vậy $A,B,O,C$  cùng thuộc đường tròn tâm N, đường kính AO.

Vì $AB,AC$  là các tiếp tuyến nên $AB=AC$  (t/c).

Mà $OA=OB$  (bán kính) nên AO là trung trực của đoạn BC.

Suy ra AO vuông góc BC