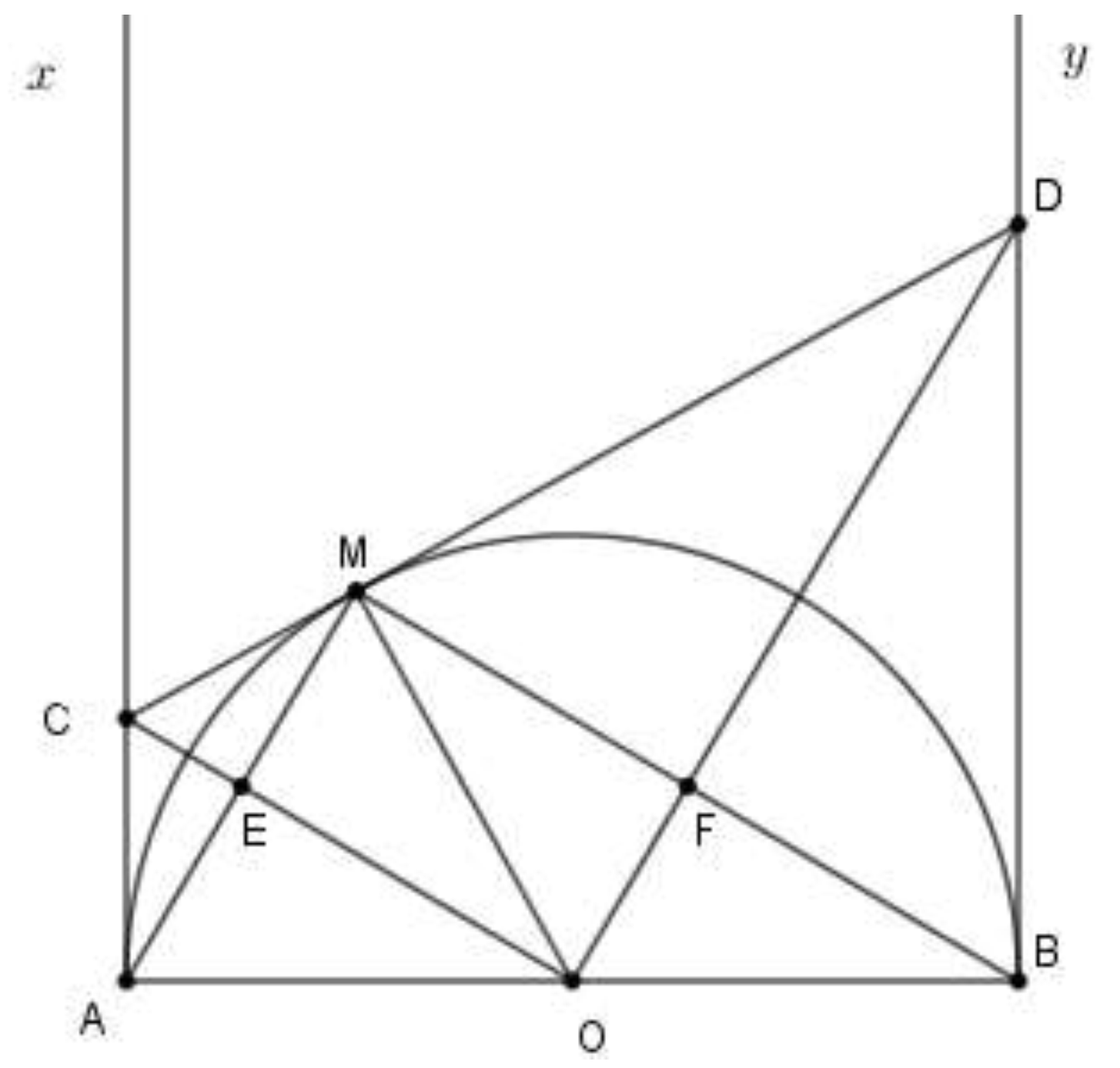
+) Xét đường tròn $\left(O\right)$  có CM và CA là hai tiếp tuyến cắt nhau nên $AC=CM$  (tính chất hai tiếp tuyến cắt nhau)

Và DM và DB là hai tiếp tuyến cắt nhau nên $DM=DB$  (tính chất hai tiếp tuyến cắt nhau)

Suy ra $AC+BD=CM+MD=CD$  (đpcm)

+) CM Tứ giác MEOF là hình chữ nhật

Ta có: $CM=CA$  (cmt); $OM=OA=R$  nên OC là đường trung trực của đoạn $AM\Rightarrow OC\perp AM$  tại $E\Rightarrow MEO=90°$ . (3)

Tương tự ta có  $MFO=90°$ (4)

Xét $\Delta AMB$  nội tiếp đường tròn $\left(O\right)$  có AB là đường kính nên $\Delta MAB$  vuông tại  $M\Rightarrow EMF=90°$ (5)

Từ (3), (4) và (5) $\Rightarrow$  tứ giác MEOF là hình chữ nhật (đpcm).