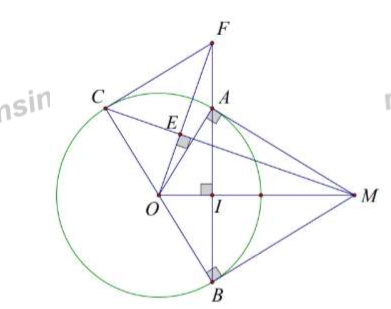
Cho đường tròn $\left(O\right)$  và một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn $\left(O\right)$  (A  và B là hai tiếp điểm). Gọi I là giao điểm của OM và AB. Kẻ đường kính BC của $\left(O\right)$ .

Chứng minh 4 điểm M,O,A,B cùng thuộc một đường tròn.

Gọi K là trung điểm $OM\Rightarrow OK=KM$ .

Tam giác OMA vuông tại A nên $AK=KM=KO=\frac{1}{2}OM$  (tính chất trung tuyến tam giác vuông).

Tam giác OBM vuông tại B nên $BK=KM=KO=\frac{1}{2}OM$  (tính chất trung tuyến tam giác vuông).

Do đó $OK=KM=KA=KB$ .

Suy ra 4 điểm $O,A,M,B$  nằm trên đường tròn tâm K, đường kính OM.