Chứng minh 2n3 +3n2 + n chia hết cho 6 với mọi số nguyên n.
Chứng minh 2n3 +3n2 + n chia hết cho 6 với mọi số nguyên n.
Ta có:
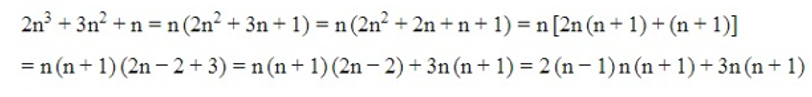
Ta thấy (n – 1), n, (n + 1) là 3 số nguyên liên tiếp
Suy ra (n – 1)n(n + 1) chia hết cho 2 và 3
Do đó 2(n – 1)n(n + 1) ⋮ 6
Có n(n + 1) ⋮ 2
Suy ra 3n(n + 1) ⋮ 6
Do đó 2(n – 1)n(n + 1) + 3n(n + 1) ⋮ 6
Vậy 2n3 +3n2 + n chia hết cho 6 với mọi số nguyên n.