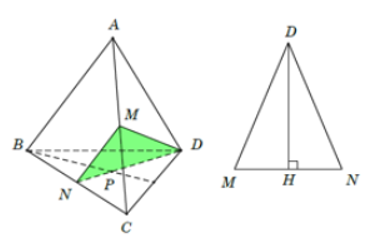
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a. Gọi M, N lần lượt là trung điểm các cạnh AC, BC; P là trọng tâm tam giác BCD. Mặt phẳng MNP cắt tứ diện theo một thiết diện có diện tích là:

A. $\frac{a^2\sqrt{11}}{2}$ ;

Đáp án đúng là C

Trong tam giác BCD có: P là trọng tâm, N là trung điểm BC

Suy ra N, P, D thẳng hàng

Vậy thiết diện là tam giác MND.

Xét tam giác MND, ta có $MN=\frac{AB}{2}=a;DM=DN=\frac{A\text{D}\sqrt{3}}{2}=a\sqrt{3}$

Do đó tam giác MND cân tại D

Gọi H là trung điểm MN suy ra DH ⊥ MN và $MH=\frac{NM}{2}=\frac{a}{2}$

Xét tam giác DMH vuông tại H có MD² = DH² + MH²

Suy ra $DH=\sqrt{M{\text{D}}^2-M{H}^2}=\sqrt{3a^2-\frac{a^2}{4}}=\frac{a\sqrt{11}}{2}$

Diện tích tam giác SMD là ${\text{S}}_{MN\text{D}}=\frac{1}{2}MN.DH=\frac{1}{2}.a.\frac{a\sqrt{11}}{2}=\frac{a^2\sqrt{11}}{4}$

Vậy ta chọn đáp án C.