Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V?

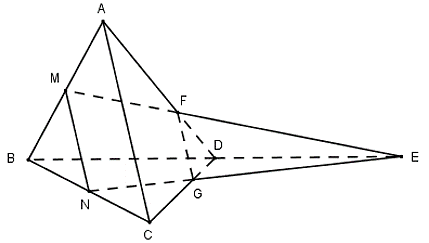
Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Gọi thể tích của phần đa diện còn lại là V'

Gọi F = EM Ç AD; G = EN Ç CD

Áp dụng định lí Menelaus trong tam giác BCD có:

$\frac{NB}{NC}.\frac{GC}{GD}.\frac{ED}{EB}=1\Rightarrow \frac{GC}{GD}=2$

 Áp dụng định lí Menelaus trong tam giác ABD có: 

$\frac{MA}{MB}.\frac{EB}{ED}.\frac{FD}{FA}=1\Rightarrow \frac{FD}{FA}=\frac{1}{2}$

Ta có:

$S_{\Delta EBN}=\frac{1}{2}d\left(E;BN\right).BN=\frac{1}{2}.2d\left(D;BC\right).\frac{1}{2}BC$

$=\frac{1}{2}.d\left(D;BC\right).BC=S_{\Delta BCD}$

Do  $d\left(M;\left(EBN\right)\right)=\frac{1}{2}d\left(A;\left(BCD\right)\right)\Rightarrow V_{M.EBN}=\frac{1}{2}{V}_{A.BCD}$

$S_{\Delta EDG}=\frac{1}{2}d\left(G;DE\right).DE=\frac{1}{2}.\frac{1}{3}d\left(C;BD\right).BD$

$=\frac{1}{3}.\frac{1}{2}d\left(C;BD\right).BD=S_{\Delta BCD}$

Do  $d\left(F;\left(EDG\right)\right)=\frac{1}{3}d\left(A;\left(BCD\right)\right)\Rightarrow V_{F.EDG}=\frac{1}{9}{V}_{A.BCD}$

Suy ra  $V\text{'}=V_{F.EDG}-V_{M.EBN}=\frac{V_{ABCD}}{2}-\frac{V_{ABCD}}{9}=\frac{7}{18}{V}_{ABCD}$

$\Rightarrow V=\frac{11}{18}{V}_{ABCD}$

Gọi H là tâm đường tròn ngoại tiếp tam giác BCD ta có:

AH ^ (BCD) và  $BH=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$

$\Rightarrow AH=\sqrt{a^2-{\left(\frac{a\sqrt{3}}{3}\right)}^2}=\frac{a\sqrt{6}}{3}$

Suy ra   $V_{ABCD}=\frac{1}{3}AH.S_{BCD}=\frac{1}{3}.\frac{a\sqrt{6}}{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{2}}{12}$

 $\Rightarrow V=\frac{11}{18}.\frac{a^3\sqrt{2}}{12}=\frac{11\sqrt{2}{a}^3}{216}$.