Cho tứ diện ABCD. Trên cạnh AB lấy điểm M sao cho BM = 3AM. Mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC

Bài 4.46 trang 103 Toán 11 Tập 1: Cho tứ diện ABCD. Trên cạnh AB lấy điểm M sao cho BM = 3AM. Mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC.

a) Xác định giao điểm K của mặt phẳng (P) với đường thẳng CD.

b) Tính tỉ số $\frac{KC}{CD}$ .

Trả lời

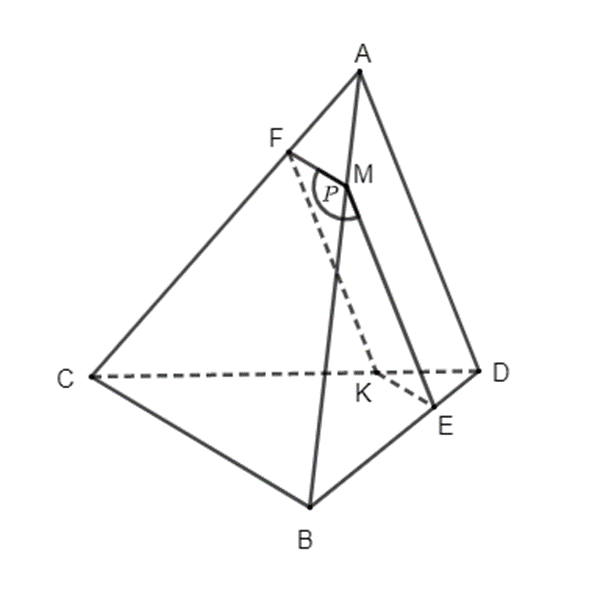
a) Trong mặt phẳng (ABD), qua M kẻ đường thẳng song song với AD cắt BD tại E.

Trong mặt phẳng (ABC), qua M kẻ đường thẳng song song với BC cắt AC tại F.

Trong mặt phẳng (ACD), qua F kẻ đường thẳng song song với AD cắt CD tại K.

Do đó, mặt phẳng (P) đi qua M song song với hai đường thẳng AD và BC là mặt phẳng (MEKF).

Vì K thuộc mặt phẳng (MEKF) nên K thuộc mặt phẳng (P).

Vậy K là giao điểm của mặt phẳng (P) và đường thẳng CD.

b) Ta có: BM + AM = AB.

Mà BM = 3AM hay AM = $\frac{1}{3}$ BM nên BM + $\frac{1}{3}$ BM = AB ⇔ $\frac{4}{3}$ BM = AB $\iff \frac{BM}{AB}=\frac{3}{4}$ .

Xét tam giác BAD có ME // AD, theo định lí Thalés ta có: $\frac{BE}{BD}=\frac{BM}{AB}=\frac{3}{4}$ .

Xét tam giác BCD có EK // BC, theo định lí Thalés ta có: $\frac{KC}{CD}=\frac{BE}{BD}=\frac{3}{4}$ .

Vậy $\frac{KC}{CD}=\frac{3}{4}$ .

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục