Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, K lần lượt là trọng tâm của các tam giác SAD, SCD. Chứng minh rằng GK // (ABCD)

Bài 4.44 trang 103 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, K lần lượt là trọng tâm của các tam giác SAD, SCD.

a) Chứng minh rằng GK // (ABCD).

b) Mặt phẳng chứa đường thẳng GK và song song với mặt phẳng (ABCD) cắt các cạnh SA, SB, SC, SD lần lượt tại M, N, E, F. Chứng minh rằng tứ giác MNEF là hình bình hành.

Trả lời

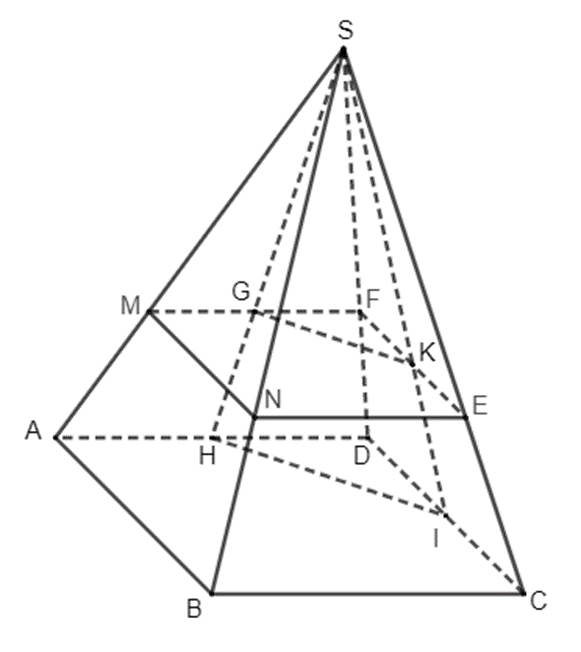
a) Gọi H, I lần lượt là trung điểm của AD và CD.

Vì G, K lần lượt là trọng tâm của các tam giác SAD, SCD nên theo tính chất trọng tâm trong tam giác ta có S, G, H thẳng hàng, S, K, I thẳng hàng và $\frac{SG}{SH}=\frac{1}{3};\frac{SK}{SI}=\frac{1}{3}$ .

Xét tam giác SHI có $\frac{SG}{SH}=\frac{SK}{SI}\left(=\frac{1}{3}\right)$ , suy ra GK // HI (định lí Thalés).

Vì H thuộc AD nên H thuộc mặt phẳng (ABCD), vì I thuộc CD nên I thuộc mặt phẳng (ABCD). Do đó, mặt phẳng (ABCD) chứa đường thẳng HI.

Đường thẳng GK song song với đường thẳng HI và đường thẳng HI nằm trong mặt phẳng (ABCD) nên GK // (ABCD).

b) Trong mặt phẳng (SAD), từ G kẻ đường thẳng song song với AD, cắt SA, SD lần lượt tại M và F, suy ra MF // AD nên MF // (ABCD).

Trong mặt phẳng (SCD), nối F với K, đường thẳng FK cắt SC tại E.

Trong mặt phẳng (SBC), từ E kẻ đường thẳng song song với BC, cắt SB tại N.

Xét tam giác SHD có GF // HD (do MF // AD), theo định lí Thalés suy ra $\frac{SF}{SD}=\frac{SG}{SH}=\frac{1}{3}$ .

Xét tam giác SDI có $\frac{SF}{SD}=\frac{SK}{SI}\left(=\frac{1}{3}\right)$ , do đó FK // DI hay EF // DC, suy ra EF // (ABCD).

Vì MF // CD, NE // BC, AD // BC nên MF // NE, suy ra bốn điểm M, N, E, F đồng phẳng.

Mặt phẳng (MNEF) chứa hai đường thẳng cắt nhau MF và EF cùng song song với mặt phẳng (ABCD). Do đó, hai mặt phẳng (MNEF) và (ABCD) song song với nhau.

Vì G thuộc MF nên G thuộc mặt phẳng (MNEF), vì K thuộc EF nên K thuộc mặt phẳng (MNEF).

Vậy mặt phẳng chứa đường thẳng GK và song song với mặt phẳng (ABCD) cắt các cạnh SA, SB, SC, SD lần lượt tại M, N, E, F là mặt phẳng (MNEF).

Xét tam giác SAD có MF // AD nên $\frac{MF}{AD}=\frac{SF}{SD}=\frac{1}{3}$ .

Xét tam giác SCD có EF // CD nên $\frac{SE}{SC}=\frac{SF}{SD}=\frac{1}{3}$ .

Xét tam giác SBC có NE // BC nên $\frac{NE}{BC}=\frac{SE}{SC}=\frac{1}{3}$ .

Do đó, $\frac{MF}{AD}=\frac{NE}{BC}\left(=\frac{1}{3}\right)$ , mà AD = BC (do ABCD là hình bình hành) nên MF = NE.

Xét tứ giác MNEF có MF = NE và MF // NE nên tứ giác MNEF là hình bình hành.

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục