Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của các cạnh BC, AD. Giả sử AB = CD = a và PQ = $\frac{a\sqrt{3}}{2}$ . Tìm số đo góc giữa hai đường thẳng AB và CD.

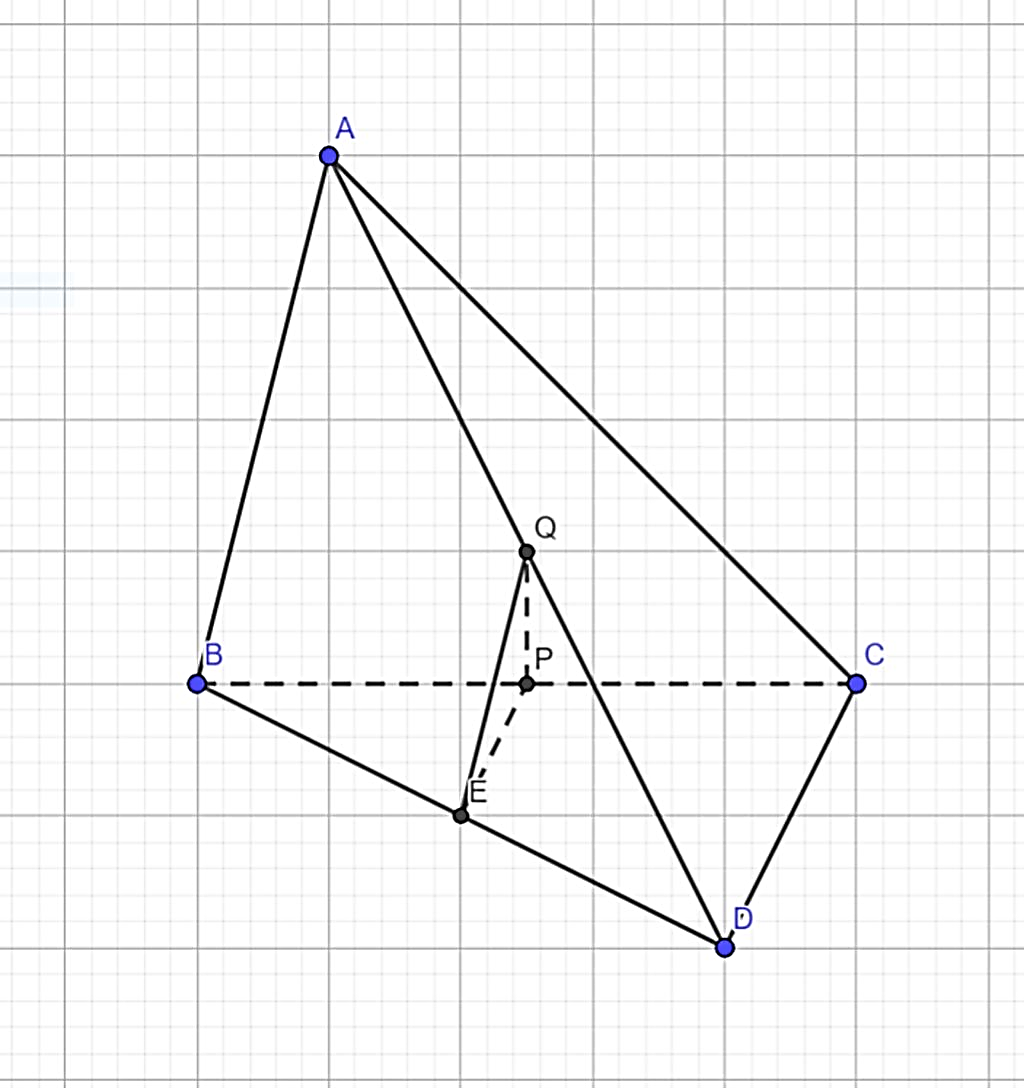
Lấy E là trung điểm BD

Ta thấy: QE, PE là đường trung bình của ∆ABD, ∆BCD

⇒ QE = $\frac{1}{2}$  AB = $\frac{1}{2}$ a, QE // AB

PE = $\frac{1}{2}$ CD = $\frac{1}{2}$  a, PE // CD

⇒ $\widehat{AB,CD}=\widehat{QE,PE}=\widehat{QEP}$

⇒ cos$\widehat{QEP}=\frac{Q{E}^2+P{E}^2-P{Q}^2}{2.PE.QE}=\frac{-1}{2}$

⇒ $\widehat{QEP}=120°$

⇒ $\widehat{QE,PE}=60°$ vì góc giữa hai đường thẳng ≤ 90°.