Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho AM/AB = AN/AC

Bài 2 trang 117 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho $\frac{AM}{AB}=\frac{AN}{AC}$; I; J lần lượt là trung điểm của BD, CD.

a) Chứng minh rằng MN // BC.

b) Tứ giác MNJI là hình gì. Tìm điểu kiện để tứ giác MNJI là hình bình hành.

Trả lời

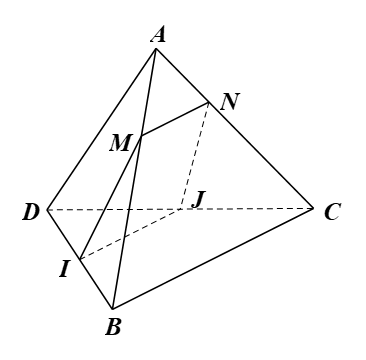
a) Xét ∆ABC có $\frac{AM}{AB}=\frac{AN}{AC}$, suy ra MN // BC (định lý Thalès đảo).

b) Xét ∆BCD có I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác DBC, suy ra IJ // BC.

Mà MN // BC (câu a) nên IJ // MN, do đó MNJI là hình thang.

MNJI là hình bình hành khi và chỉ khi MI // NJ // AD

Suy ra MI là đường trung bình của tam giác ADB.

Mà I là trung điểm của BD nên M là trung điểm AB.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3