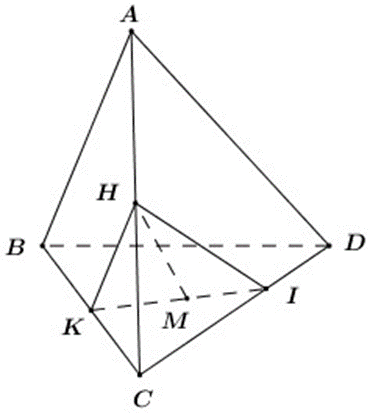
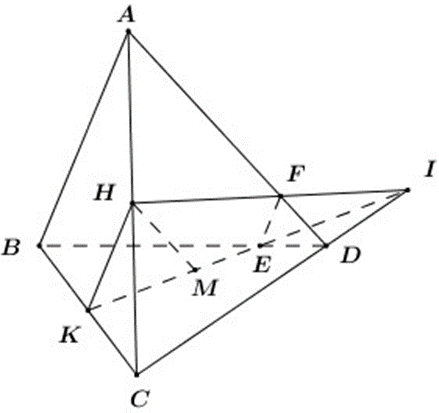
Cho tứ diện ABCD. Gọi H, K lần lượt là trung điểm của các cạnh AC, BC. Trong tam giác BCD lấy điểm M sao cho hai đường thẳng KM và CD cắt nhau tại I. Tìm thiết diện của tứ diện với (HKM) trong hai trường hợp:
a) I nằm trong đoạn CD.
b) I nằm ngoài đoạn CD.
a) I nằm trong đoạn CD
Dễ thấy \((HKM) \equiv (HKI)\) và (HKM) đã khép kín và cắt tất cả các mặt của hình chóp lần lượt theo các giao tuyến sau:
\(\begin{array}{l}(HKM) \cap (ABC) = HK\\(HKM) \cap (BCD) = KI\\(HKM) \cap (ACD) = IH\end{array}\)
Vậy thiết diện của hình chóp khi cắt bởi (HKM) là tam giác HKM.
b) I nằm ngoài đoạn CD
+ Bước 1: Giao tuyến có sẵn HK
+ Bước 2: \((HKM) \equiv (HKI)\)
Trong (BCD) gọi giao điểm của KI và BD là E
Trong (ACD) gọi giao điểm của HI và AD là F
+ Bước 3 : Lúc này mặt (HKM) đã khép kín và cắt tất cả các mặt của hình chóp lần lượt theo các giao tuyến sau:
\(\begin{array}{l}(HKM) \cap (ABC) = HK\\(HKM) \cap (BCD) = KE\\(HKM) \cap (ABD) = EF\\(HKM) \cap (ACD) = FH\end{array}\)
Vậy thiết diện của hình chóp khi cắt bởi (HKM) là tứ giác HKEF.