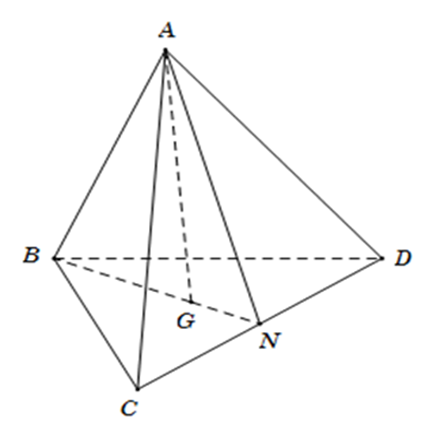
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là:
A. AM (M là trung điểm của AB)
B. AN (N là trung điểm của CD)
C. AH (H là hình chiếu của B trên CD)
D. AK (K là hình chiếu của C trên BD).
Đáp án đúng là: B
Gọi giao điểm của BG và CD là N
Ta có \(\left\{ \begin{array}{l}N \in BG \subset \left( {ABG} \right) \Rightarrow N \in \left( {ABG} \right)\\N \in C{\rm{D}} \subset \left( {AC{\rm{D}}} \right) \Rightarrow N \in \left( {AC{\rm{D}}} \right)\end{array} \right.\)
Suy ra N là điểm chung giữa hai mặt phẳng (ACD) và (GAB) và N là trung điểm của CD do G là trong tâm của tam giác BCD
Mà A là 1 điểm chung giữa hai mặt phẳng (ACD) và (GAB)
Suy ra (ACD) ∩ (GAB) = AN
Vậy ta chọn đáp án B.