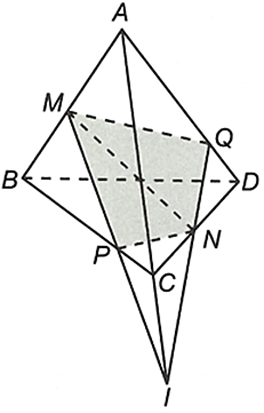
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).