Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau AB = 6a, AC = 7a, AD = 4a. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích của tứ diện AMNP.
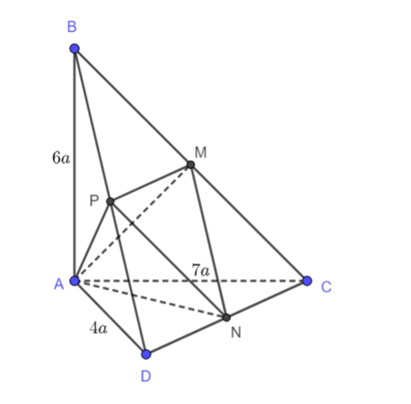
VABCD = \(\frac{1}{3}.6a.\frac{1}{2}.7a.4a = 28{a^3}\)
\[\frac{{{V_{APMN}}}}{{{V_{ABCD}}}} = \frac{{\frac{1}{3}.d\left( {A,\left( {PMN} \right)} \right).{S_{PMN}}}}{{\frac{1}{3}.d\left( {A,\left( {BCD} \right)} \right).{S_{BCD}}}}\] (do mặt phẳng (PMN) chính là mặt phẳng (BCD) nên d(A,(PMN) = d(A,(BCD))
⇒ \[\frac{{{V_{APMN}}}}{{{V_{ABCD}}}} = \frac{{\frac{1}{3}.d\left( {A,\left( {PMN} \right)} \right).{S_{PMN}}}}{{\frac{1}{3}.d\left( {A,\left( {BCD} \right)} \right).{S_{BCD}}}} = \frac{{{S_{PMN}}}}{{{S_{BCD}}}}\]
Mà \[\frac{{{S_{PMN}}}}{{{S_{BCD}}}} = \frac{{\frac{1}{2}.PM.PN.\sin \left( {\widehat {PM,PN}} \right)}}{{\frac{1}{2}.DC.BC.\sin \left( {\widehat {DC,BC}} \right)}}\] (do PM, MN là đường trung bình của tam giác BCD, PNCM là hình bình hành nên \(\widehat {NPM} = \widehat {BCD}\)
Suy ra: \[\frac{{{V_{APMN}}}}{{{V_{ABCD}}}} = \frac{{{S_{PMN}}}}{{{S_{BCD}}}} = \frac{{PM.PN}}{{DC.BC}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\]
VAMNP = \(\frac{1}{4}.28{a^3} = 7{a^3}\).