Cho ∆ABC vuông tại A (AB < AC), đường cao AH. Gọi M là trung điểm của BC, D là điểm đối xứng với A qua M. trên tia đối của tia HA lấy điểm E sao cho HE = HA.
a) Chứng minh HM // ED và HM =\(\frac{1}{2}\)DE.
b) Chứng minh ABDC là hình chữ nhật.
c) Gọi P, Q lần lượt là hình chiếu của E lên BD và CD, EP cắt AD tại K. Chứng minh DE = DK.
d) Chứng minh 3 điểm H, P, Q thẳng hàng.
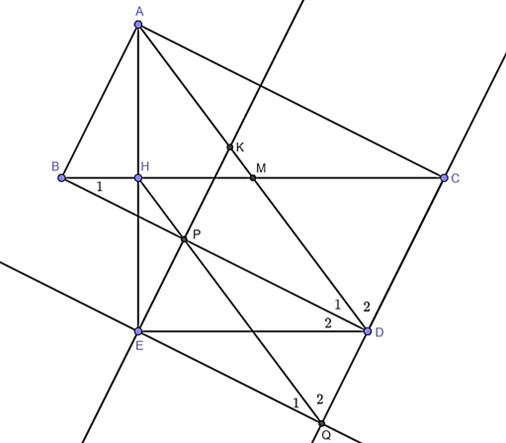
a) Vì AH = HE và AM = MD
⇒ HM là đường trung bình của ΔABC
⇒ HM // ED và HM = \(\frac{1}{2}\)DE
b) Vì AM = MD và BM = MC
⇒ ABCD là hình bình hành
Mà \(\widehat {BAC} = 90^\circ \) ⇒ ABCD là hình chữ nhật
c) Vì ABCD là hình chữ nhật
⇒ \(\widehat {BDA} = 90^\circ \)
Vì ED // BC ⇒ \(\widehat {CBD} = 90^\circ \)
⇒ \(\widehat {BDA} = \widehat {CBD} = 90^\circ \)
Xét tam giác KPD và tam giác EPD có:
\(\widehat {KPD} = \widehat {EPD} = 90^\circ \)
PD là cạnh chung
\(\widehat {KDP} = \widehat {EDP} = 45^\circ \)
⇒ ΔKPD = ΔEPD (g.c.g)
⇒ DE = DK(2 cạnh tương ứng)
d) Vì EP = PK và EH = AH
⇒ HP là đường trung bình của ΔAEK
⇒ HP // AD (1)
Tứ giác EPDQ có 3 góc vuông tại đỉnh P, D, Q
⇒ EPDQ là hình chữ nhật
⇒ \(\widehat {{Q_1}} = \widehat {{D_2}}\)
Mà \(\widehat {{D_1}} = \widehat {{D_2}}\)
⇒ \[\widehat {{Q_1}} = \widehat {{D_1}}\]
⇒ \(\widehat {{Q_2}} = \widehat {{D_2}}\)(cùng phụ với hai góc bằng nhau)
⇒ PQ // AD (2)
Từ (1) và (2) ⇒ HP // AD
⇒ H, P, Q thẳng hàng.