Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt
Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H (D Î BC, E Î AC, F Î AB). Chứng minh các tứ giác BDHF, BFEC nội tiếp.
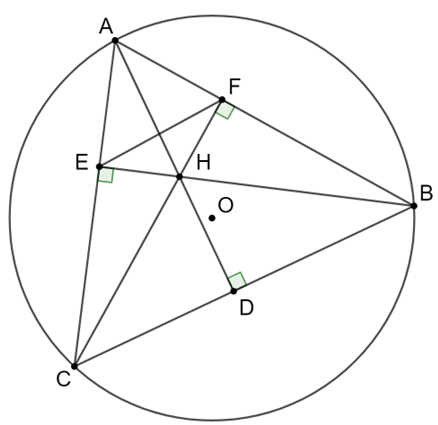
a) Ta có: \(AD \bot BC \Rightarrow \widehat {ADB} = 90^\circ \Rightarrow \widehat {HDB} = 90^\circ \) (1)
\(CF \bot AB \Rightarrow \widehat {CFB} = 90^\circ \Rightarrow \widehat {HFB} = 90^\circ \) (2)
Từ (1) và (2), ta thấy \(\widehat {HDB} + \widehat {HFB} = 90^\circ + 90^\circ = 180^\circ \)
Tứ giác BDHF có tổng hai góc đối bằng 180°.
Vậy tứ giác BDHF nội tiếp.
Ta có: \(BE \bot AC \Rightarrow \widehat {BEC} = 90^\circ \) (3)
\(CF \bot AB \Rightarrow \widehat {CFB} = 90^\circ \) (4)
Từ (3) và (4), ta thấy \(\widehat {BEC} = \widehat {CFB} = 90^\circ \).
Tứ giác BDHF có hai góc cùng chắn cung bằng nhau.
Vậy tứ giác BFCE nội tiếp.