Câu hỏi:
01/02/2024 51Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Khẳng định nào dưới đây là đúng:
A. \(\widehat {NIH} = \widehat {PIH}\);
B. IM = IN = IP;
C. \(\widehat {NIH} = \widehat {PIA}\);
D. IA = IB = IC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
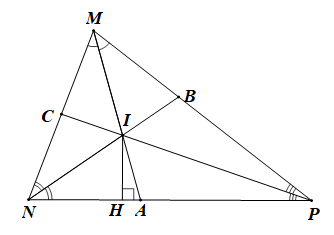
Xét DMNP có ba đường phân giác MA, NB, PC cắt nhau tại I nên I cách đều ba cạnh của tam giác.
Điểm I không phải là giao điểm ba đường trung trực của tam giác nên không cách đều ba đỉnh. Do đó phương án B, D là sai.
Vì MI là tia phân giác của góc NMP nên \(\widehat {NMI} = \widehat {PMI} = \frac{1}{2}\widehat {PMN}\).
Vì NI là tia phân giác của góc MNP nên \(\widehat {MNI} = \widehat {PNI} = \frac{1}{2}\widehat {MNP}\).
Vì PI là đường phân giác của góc MPN nên \(\widehat {NPI} = \widehat {MPI} = \frac{1}{2}\widehat {MPN}\).
Xét DMIP có \(\widehat {MIP} + \widehat {MPI} + \widehat {PMI} = 180^\circ \) (tổng ba góc trong một tam giác)
Nên \(\widehat {MIP} = 180^\circ - \left( {\widehat {MPI} + \widehat {PMI}} \right)\)
Suy ra \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {\widehat {MPN} + \widehat {PMN}} \right)\).
Xét DMNP có \(\widehat {MNP} + \widehat {MPN} + \widehat {PMN} = 180^\circ \)(tổng ba góc trong một tam giác)
Nên \(\widehat {MPN} + \widehat {PMN} = 180^\circ - \widehat {MNP}\).
Do đó \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {MNP}} \right)\)
Hay \(\widehat {MIP} = 180^\circ - 90^\circ + \frac{1}{2}\widehat {MNP} = 90^\circ + \frac{1}{2}\widehat {MNP}\).
Ta có \(\widehat {MIP} + \widehat {PIA} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {PIA} = 180^\circ - \widehat {MIP} = 180^\circ - \left( {90^\circ + \frac{1}{2}\widehat {MNP}} \right) = 90^\circ - \frac{1}{2}\widehat {MNP}\) (1)
Vì DINH vuông tại H nên \(\widehat {HIN} + \widehat {HNI} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {HIN} = 90^\circ - \widehat {HNI} = 90^\circ - \frac{1}{2}\widehat {MNP}\) (2)
Từ (1) và (2) suy ra \(\widehat {NIH} = \widehat {PIA}\).
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C

Xét DMNP có ba đường phân giác MA, NB, PC cắt nhau tại I nên I cách đều ba cạnh của tam giác.
Điểm I không phải là giao điểm ba đường trung trực của tam giác nên không cách đều ba đỉnh. Do đó phương án B, D là sai.
Vì MI là tia phân giác của góc NMP nên \(\widehat {NMI} = \widehat {PMI} = \frac{1}{2}\widehat {PMN}\).
Vì NI là tia phân giác của góc MNP nên \(\widehat {MNI} = \widehat {PNI} = \frac{1}{2}\widehat {MNP}\).
Vì PI là đường phân giác của góc MPN nên \(\widehat {NPI} = \widehat {MPI} = \frac{1}{2}\widehat {MPN}\).
Xét DMIP có \(\widehat {MIP} + \widehat {MPI} + \widehat {PMI} = 180^\circ \) (tổng ba góc trong một tam giác)
Nên \(\widehat {MIP} = 180^\circ - \left( {\widehat {MPI} + \widehat {PMI}} \right)\)
Suy ra \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {\widehat {MPN} + \widehat {PMN}} \right)\).
Xét DMNP có \(\widehat {MNP} + \widehat {MPN} + \widehat {PMN} = 180^\circ \)(tổng ba góc trong một tam giác)
Nên \(\widehat {MPN} + \widehat {PMN} = 180^\circ - \widehat {MNP}\).
Do đó \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {MNP}} \right)\)
Hay \(\widehat {MIP} = 180^\circ - 90^\circ + \frac{1}{2}\widehat {MNP} = 90^\circ + \frac{1}{2}\widehat {MNP}\).
Ta có \(\widehat {MIP} + \widehat {PIA} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {PIA} = 180^\circ - \widehat {MIP} = 180^\circ - \left( {90^\circ + \frac{1}{2}\widehat {MNP}} \right) = 90^\circ - \frac{1}{2}\widehat {MNP}\) (1)
Vì DINH vuông tại H nên \(\widehat {HIN} + \widehat {HNI} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {HIN} = 90^\circ - \widehat {HNI} = 90^\circ - \frac{1}{2}\widehat {MNP}\) (2)
Từ (1) và (2) suy ra \(\widehat {NIH} = \widehat {PIA}\).
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến AB, AC, BC. Biết KI = 5 cm, BK = 10 cm, KC = 15 cm. Diện tích tam giác ABC bằng:
Câu 2:
Cho tam giác IHK có hai tia phân giác của góc H và góc K cắt nhau tại O. Khẳng định nào sau đây là đúng?


