Câu hỏi:
01/02/2024 48Cho tam giác IHK có hai tia phân giác của góc H và góc K cắt nhau tại O. Khẳng định nào sau đây là đúng?
A. \(\widehat {I{\rm{O}}K} = 90^\circ - \frac{1}{2}\widehat {IHK}\);
B. \(\widehat {I{\rm{O}}K} = 90^\circ + \frac{1}{2}\widehat {IHK}\);
C. \(\widehat {I{\rm{O}}K} = 180^\circ - \frac{1}{2}\widehat {IHK}\);
D. \(\widehat {I{\rm{O}}K} = 180^\circ + \frac{1}{2}\widehat {IHK}\).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
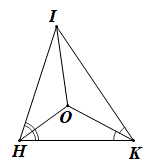
Vì DIHK có hai tia phân giác của góc H và góc K cắt nhau tại O nên IO là tia phân giác của góc HIK.
Do đó \(\widehat {HIO} = \widehat {KIO} = \frac{1}{2}\widehat {HIK}\).
Vì KO là tia phân giác của góc HKI nên \(\widehat {HKO} = \widehat {IKO} = \frac{1}{2}\widehat {HKI}\).
Xét DOIK có \(\widehat {IKO} + \widehat {KIO} + \widehat {KOI} = 180^\circ \) (tổng ba góc trong một tam giác)
Nên \(\widehat {KOI} = 180^\circ - \left( {\widehat {IKO} + \widehat {KIO}} \right)\)
Suy ra \(\widehat {KOI} = 180^\circ - \frac{1}{2}\left( {\widehat {HKI} + \widehat {KIH}} \right)\)
Lại có \(\widehat {HKI} + \widehat {KIH} = 180^\circ - \widehat {IHK}\) (tổng ba góc trong tam giác HIK)
Nên \(\widehat {KOI} = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {IHK}} \right) = 180^\circ - 90^\circ + \frac{1}{2}\widehat {IHK} = 90^\circ + \frac{1}{2}\widehat {IHK}\)
Vậy ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: B
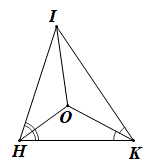
Vì DIHK có hai tia phân giác của góc H và góc K cắt nhau tại O nên IO là tia phân giác của góc HIK.
Do đó \(\widehat {HIO} = \widehat {KIO} = \frac{1}{2}\widehat {HIK}\).
Vì KO là tia phân giác của góc HKI nên \(\widehat {HKO} = \widehat {IKO} = \frac{1}{2}\widehat {HKI}\).
Xét DOIK có \(\widehat {IKO} + \widehat {KIO} + \widehat {KOI} = 180^\circ \) (tổng ba góc trong một tam giác)
Nên \(\widehat {KOI} = 180^\circ - \left( {\widehat {IKO} + \widehat {KIO}} \right)\)
Suy ra \(\widehat {KOI} = 180^\circ - \frac{1}{2}\left( {\widehat {HKI} + \widehat {KIH}} \right)\)
Lại có \(\widehat {HKI} + \widehat {KIH} = 180^\circ - \widehat {IHK}\) (tổng ba góc trong tam giác HIK)
Nên \(\widehat {KOI} = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {IHK}} \right) = 180^\circ - 90^\circ + \frac{1}{2}\widehat {IHK} = 90^\circ + \frac{1}{2}\widehat {IHK}\)
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Khẳng định nào dưới đây là đúng:
Câu 2:
Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến AB, AC, BC. Biết KI = 5 cm, BK = 10 cm, KC = 15 cm. Diện tích tam giác ABC bằng:


