Cho tam giác đều DEF có độ dài cạnh bằng 9cm. Khi đó bán kính đường tròn ngoại
Cho tam giác đều DEF có độ dài cạnh bằng 9cm. Khi đó bán kính đường tròn ngoại tiếp tam giác DEF bằng?
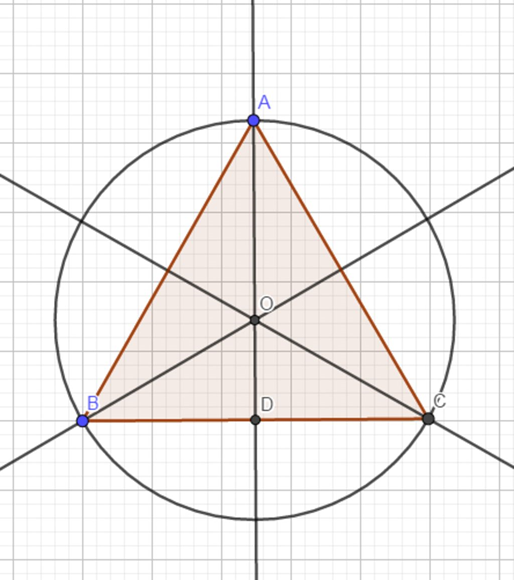
Do là tam giác đều nên yrọng tâm trùng trực tâm và là tâm đường tròn
Gọi AO ∩ BC = D
Áp dụng định lí py–ta–go vào tam giác ADC , ta có :
AC2 = AD2 + DC2
AD = \(\sqrt {A{C^2} - D{C^2}} = \frac{{9\sqrt 3 }}{2}\)
Mà AO = \(\frac{2}{3}AD\) do O là trọng tâm tam giác ABC
AO = \(\frac{2}{3}.\frac{{9\sqrt 3 }}{2} = \frac{{9\sqrt 3 }}{3} = 3\sqrt 3 \).