Câu hỏi:
01/02/2024 43Cho tam giác DEG cân tại D có H là trực tâm. Biết \(\widehat {EHG} = 136^\circ \). Số đo các góc D, E, G lần lượt là:
A. 68°, 68°, 68°;
B. 68°, 68°, 44°;
C. 44°, 68°, 68°;
D. 44°, 44°, 68°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
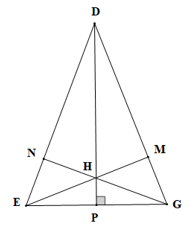
• Gọi giao điểm của DH với EG là P, giao điểm của EH với DG là M, giao điểm của GH với DE là N.
Vì H là trực tâm tam giác DEG nên DP, EM, GN là ba đường cao.
Xét DEHG có \(\widehat {HEG} + \widehat {EHG} + \widehat {HGE} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {HEG} + \widehat {HGE} = 180^\circ - \widehat {EHG} = 180^\circ - 136^\circ = 44^\circ \).
• Xét DENG và DGME có:
\(\widehat {ENG} = \widehat {GME}( = 90^\circ )\)
EG là cạnh chung,
\(\widehat {NEG} = \widehat {MGE}\) (do DDEG cân tại D)
Suy ra ΔENG = ∆GME (cạnh huyền – góc nhọn).
Do đó \(\widehat {NGE} = \widehat {MEG}\) (hai góc tương ứng)
Mà \(\widehat {NGE} + \widehat {MEG} = 44^\circ \) (do \(\widehat {HGE} + \widehat {HEG} = 44^\circ \))
Suy ra \(\widehat {NGE} = \widehat {MEG} = 22^\circ \)
Vì DMEG vuông tại M nên \(\widehat {MGE} + \widehat {MEG} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {MGE} = 90^\circ - \widehat {MEG} = 90^\circ - 22^\circ = 68^\circ \) hay \(\widehat {DGE} = 68^\circ \).
Mà \(\widehat {DEG} = \widehat {DGE}\)(do DDEG cân tại D) nên \(\widehat {DEG} = 68^\circ \).
Xét DEDG có \(\widehat {DGE} + \widehat {EDG} + \widehat {DEG} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {EDG} = 180^\circ - \widehat {DEG} - \widehat {DGE} = 180^\circ - 68^\circ - 68^\circ = 44^\circ \).
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C

• Gọi giao điểm của DH với EG là P, giao điểm của EH với DG là M, giao điểm của GH với DE là N.
Vì H là trực tâm tam giác DEG nên DP, EM, GN là ba đường cao.
Xét DEHG có \(\widehat {HEG} + \widehat {EHG} + \widehat {HGE} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {HEG} + \widehat {HGE} = 180^\circ - \widehat {EHG} = 180^\circ - 136^\circ = 44^\circ \).
• Xét DENG và DGME có:
\(\widehat {ENG} = \widehat {GME}( = 90^\circ )\)
EG là cạnh chung,
\(\widehat {NEG} = \widehat {MGE}\) (do DDEG cân tại D)
Suy ra ΔENG = ∆GME (cạnh huyền – góc nhọn).
Do đó \(\widehat {NGE} = \widehat {MEG}\) (hai góc tương ứng)
Mà \(\widehat {NGE} + \widehat {MEG} = 44^\circ \) (do \(\widehat {HGE} + \widehat {HEG} = 44^\circ \))
Suy ra \(\widehat {NGE} = \widehat {MEG} = 22^\circ \)
Vì DMEG vuông tại M nên \(\widehat {MGE} + \widehat {MEG} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {MGE} = 90^\circ - \widehat {MEG} = 90^\circ - 22^\circ = 68^\circ \) hay \(\widehat {DGE} = 68^\circ \).
Mà \(\widehat {DEG} = \widehat {DGE}\)(do DDEG cân tại D) nên \(\widehat {DEG} = 68^\circ \).
Xét DEDG có \(\widehat {DGE} + \widehat {EDG} + \widehat {DEG} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {EDG} = 180^\circ - \widehat {DEG} - \widehat {DGE} = 180^\circ - 68^\circ - 68^\circ = 44^\circ \).
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC nhọn có BM và CN là hai đường cao. Trên tia đối của BM lấy P sao cho BP = AC, trên tia đối của CN lấy Q sao cho CQ = AB. Chọn khẳng định đúng?
Câu 2:
Cho tam giác ABC vuông cân tại A. Trên cạnh AC lấy điểm E sao cho góc ABE bằng 30°. Trên tia đối của tia AB lấy F sao cho AF = AE. Vẽ điểm I sao cho FC là trung trực của EI. Số đo góc BFI là:


