Câu hỏi:
01/02/2024 47
Cho tam giác ABC nhọn có BM và CN là hai đường cao. Trên tia đối của BM lấy P sao cho BP = AC, trên tia đối của CN lấy Q sao cho CQ = AB. Chọn khẳng định đúng?
A. AP = AQ;
B. AP < AQ;
C. AP > AQ;
D. AP = 2AQ.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
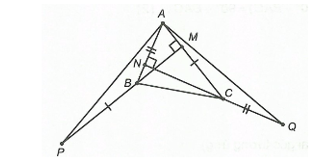
Vì DABM vuông tại M nên nên \(\widehat {MAB} + \widehat {MBA} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Vì DACN vuông tại N nên nên \(\widehat {NAC} + \widehat {NCA} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {MAB} + \widehat {MBA} = \widehat {NAC} + \widehat {NCA}\)
Do đó \(\widehat {MBA} = \widehat {NCA}\) (1)
Ta có \(\widehat {PBA} + \widehat {MBA} = 180^\circ \) (hai góc kề bù)
\(\widehat {QCA} + \widehat {NCA} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {PBA} + \widehat {MBA} = \widehat {QCA} + \widehat {NCA}\) (2)
Từ (1) và (2) suy ra \(\widehat {PBA} = \widehat {QCA}\)
Xét DABP và DQCA có
AB = CQ (giả thiết),
\(\widehat {PBA} = \widehat {ACQ}\) (chứng minh trên),
BP = AC (giả thiết)
Suy ra ΔABP = ∆QCA (c.g.c)
Do đó AP = AQ (hai cạnh tương ứng).
Vậy ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A

Vì DABM vuông tại M nên nên \(\widehat {MAB} + \widehat {MBA} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Vì DACN vuông tại N nên nên \(\widehat {NAC} + \widehat {NCA} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {MAB} + \widehat {MBA} = \widehat {NAC} + \widehat {NCA}\)
Do đó \(\widehat {MBA} = \widehat {NCA}\) (1)
Ta có \(\widehat {PBA} + \widehat {MBA} = 180^\circ \) (hai góc kề bù)
\(\widehat {QCA} + \widehat {NCA} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {PBA} + \widehat {MBA} = \widehat {QCA} + \widehat {NCA}\) (2)
Từ (1) và (2) suy ra \(\widehat {PBA} = \widehat {QCA}\)
Xét DABP và DQCA có
AB = CQ (giả thiết),
\(\widehat {PBA} = \widehat {ACQ}\) (chứng minh trên),
BP = AC (giả thiết)
Suy ra ΔABP = ∆QCA (c.g.c)
Do đó AP = AQ (hai cạnh tương ứng).
Vậy ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông cân tại A. Trên cạnh AC lấy điểm E sao cho góc ABE bằng 30°. Trên tia đối của tia AB lấy F sao cho AF = AE. Vẽ điểm I sao cho FC là trung trực của EI. Số đo góc BFI là:
Câu 2:
Cho tam giác DEG cân tại D có H là trực tâm. Biết \(\widehat {EHG} = 136^\circ \). Số đo các góc D, E, G lần lượt là:


