Cho tam giác ABC vuông tại C. Gọi D là trung điểm của AB. Kẻ DM vuông góc với AC (M thuộc AC). Gọi E là điểm đối xứng với D qua BC, DE cắt BC tại N.
a) Chứng minh tứ giác CMDN là hình chữ nhật.
b) Tứ giác BDCE là hình gì? Vì sao?
c) Chứng minh: SABC= 2 SCMDN.
d) Tam giác ABC cần có thêm điều kiện gì để tứ giác ABEC là hình thang cân?
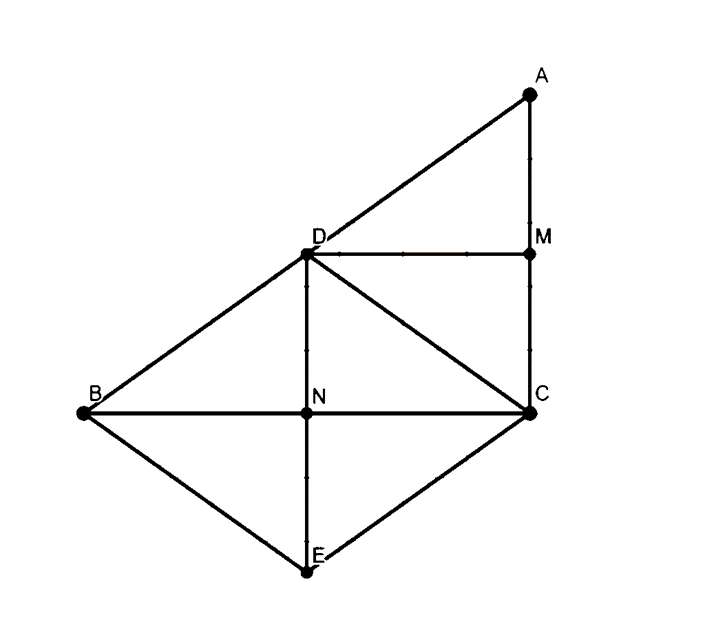
a) Ta có DM ⊥ AC, DN ⊥ BC, AC ⊥ BC
⇒ CMDN là hình chữ nhật
b) Ta có D, E đối xứng qua BC
⇒ BC là trung trực của DE
⇒ BE = CE,CE = CD
Ta có ΔABC vuông tại C, D là trung điểm AB
⇒ DB = DC = DA
⇒ EB = BD = DC = CE
⇒ CEBD là hình thoi
c) Ta có DM ⊥ AC, AC ⊥ BC ⇒ DM // CB
Mà D là trung điểm AB ⇒ DM là đường trung bình ΔABC
⇒ M là trung điểm AC ⇒ CM = \(\frac{1}{2}\)CA
Tương tự N là trung điểm BC ⇒ CN = \(\frac{1}{2}\)CB
Lại có DMCN là hình chữ nhật
⇒ SDMCN = CM.CN = \(\frac{1}{2}CA.\frac{1}{2}CB = \frac{1}{2}{S_{ABC}}\)
⇒ SABC = 2SCMDN
d) Ta có CEBD là hình thoi
⇒ CE // BD ⇒ CE // AB
⇒ CEBA là hình thang
Để ABEC là hình thang cân
⇒ \(\widehat {EBA} = \widehat {BAC}\)
⇒ \(\widehat {EBD} = \widehat {BAC}\)
⇒ \(\widehat {2CBD} = \widehat {BAC}\) vì BDCE là hình thoi
⇒ \(\widehat {2CBD} = \widehat {BAC}\)
Mà ΔABC vuông tại C ⇒ \(\widehat {BAC} = 60^\circ \).