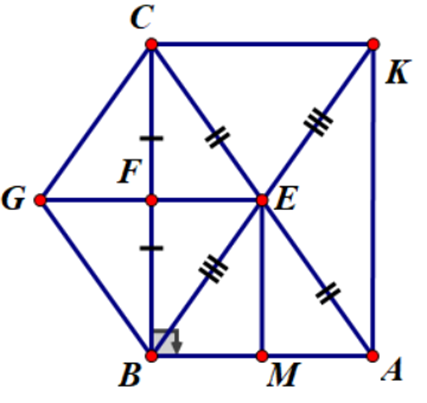
Cho tam giác ABC vuông tại B. Gọi E, F lần lượt là trung điểm của AC,BC. Kẻ Ex song song với BC cắt AB tại M
a) Chứng minh BMEF là hình chữ nhật
b) Gọi K đối xứng với B qua E. Tứ giác BAKC là hình gì? Vì sao?
c) Gọi G đối xứng với E qua F. Tứ giác BGCE là hình gì? Vì sao?
d) Tam giác ABC cần thêm điều kiện gì để tứ giác BGCE là hình vuông?
a) BE = CF, CE = EA
⇒ EF là đường trung bình tam giác ABC
⇒ EF = \(\frac{1}{2}\)AB; EF // AB
⇒ EF // BM
Mà ME // BF nên BMEF là hình bình hành
Mà \(\widehat {ABC} = 90^\circ \) nên BMEF là hình chữ nhật
b) \(\left\{ \begin{array}{l}BE = EK\\AE = EC\\\widehat {ABC} = 90^\circ \end{array} \right.\)⇒ BACK là hình chữ nhật
c) \(\left\{ \begin{array}{l}EF = FG\\CF = BF\end{array} \right.\)⇒ BGCE là hình bình hành
Mà CE = BE (tính chất hình chữ nhật BAKC)
Vậy BGCE là hình thoi.
d) BGCE là hình vuông ⇔ \(\widehat {CEB} = 90^\circ \) ⇔ CE vuông góc BE
⇔ BE là đường cao tam giác ABC
Mà BE là trung tuyến tam giác ABC
Do đó tam giác ABC phải vuông cân
Vậy BGCE là hình vuông ⇔ tam giác ABC vuông cân.